题目内容
已知圆的直径端点为A（x1，y1），B（x2，y2），求证：该圆的方程为（x-x1）（x-x2）+（y-y1）（y-y2）=0．
考点：圆的一般方程
专题：直线与圆
分析：设圆上任意一点为P（x，y），可得
=（x-x1，y-y1），
=（x-x2，y-y2），由圆的性质可得
•
=0，代入数据可得．
| PA |
| PB |
| PA |
| PB |
解答：
证明：设圆上任意一点为P（x，y），
则
=（x-x1，y-y1），
=（x-x2，y-y2），
由圆的性质可得
•
=0，
∴（x-x1）（x-x2）+（y-y1）（y-y2）=0，
∴该圆的方程为（x-x1）（x-x2）+（y-y1）（y-y2）=0
则
| PA |
| PB |
由圆的性质可得
| PA |
| PB |
∴（x-x1）（x-x2）+（y-y1）（y-y2）=0，
∴该圆的方程为（x-x1）（x-x2）+（y-y1）（y-y2）=0
点评：本题考查圆的直径式方程，涉及向量的数量积与垂直关系，属基础题．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
若函数f（x）=ex（x≤0）的反函数为y=f-1（x），则函数y=f-1（2x-1）的定义域为（ ）
| A、（0，1] | ||
| B、（-1，1] | ||
C、（-∞，
| ||
D、（
|
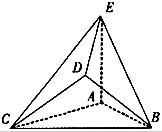在如图所示的几何体中，是边长为2的正三角形，AE＞1，AE⊥平面ABC，平面BCD⊥平面ABC，BD=CD，且BD⊥CD．
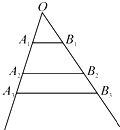如图，互不相同的点A1，A2，…，An，…和B1，B2，…，Bn，…分别在角O的两条边上，所有AnBn相互平行，且所有梯形AnBnBn+1An+1的面积均相等．设OAn=an，若a1=1，a2=2，则a9=