题目内容
江岸边有一炮台高30m,江中有两条船,船与炮台底部在同一水面上,由炮台顶部测得俯角分别为45°和60°,而且两条船与炮台底部连线成30°角,则两条船相距 m.
考点:余弦定理的应用
专题:计算题,解三角形
分析:利用直线与平面所以及俯角的定义,化为两个特殊直角三角形的计算,再在底面△BCD中用余弦定理即可求出两船距离.
解答:
解:如图,过炮台顶部A作水平面的垂线,垂足为B,设A处观测小船C的俯角为45°,
设A处观测小船D的俯角为60°,连接BC、BD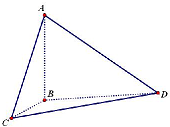
Rt△ABC中,∠ACB=45°,可得BC=AB=30米
Rt△ABD中,∠ADB=60°,可得BD=
=10
米
在△BCD中,BC=30米,BD=10
米,∠CBD=30°,
由余弦定理可得:
CD2=BC2+BD2-2BC•BDcos30°=300
∴CD=10
米(负值舍去)
故答案为:10
.
设A处观测小船D的俯角为60°,连接BC、BD

Rt△ABC中,∠ACB=45°,可得BC=AB=30米
Rt△ABD中,∠ADB=60°,可得BD=
| AB | ||
|
| 3 |
在△BCD中,BC=30米,BD=10
| 3 |
由余弦定理可得:
CD2=BC2+BD2-2BC•BDcos30°=300
∴CD=10
| 3 |
故答案为:10
| 3 |
点评:本题给出实际应用问题,求炮台旁边两条小船距的距离.着重考查了余弦定理、空间线面的位置关系等知识,属于中档题.熟练掌握直线与平面所成角的定义与余弦定理解三角形,是解决本题的关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
下列四个命题中,其中正确的命题的是( )
| A、过三点确定一个平面 |
| B、矩形是平面图形 |
| C、四边相等的四边形是平面图形 |
| D、三条直线两两相交则确定一个平面 |
下列四个函数中,在(0,+∞)上为增函数的是( )
| A、f(x)=3-x | ||
| B、f(x)=x2-3x | ||
| C、f(x)=-x2 | ||
D、f(x)=-
|
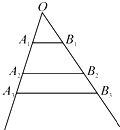 如图,互不相同的点A1,A2,…,An,…和B1,B2,…,Bn,…分别在角O的两条边上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等.设OAn=an,若a1=1,a2=2,则a9=
如图,互不相同的点A1,A2,…,An,…和B1,B2,…,Bn,…分别在角O的两条边上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等.设OAn=an,若a1=1,a2=2,则a9=