题目内容
曲线y=
与直线x=1，x=e2及x轴所围成的图形的面积是（ ）
| 1 |
| x |
| A、e2 |
| B、e2-1 |
| C、e |
| D、2 |
考点：定积分在求面积中的应用
专题：计算题,导数的概念及应用
分析：确定被积区间及被积函数，利用定积分表示面积，即可得到结论．
解答：
解：由题意，由曲线y=
与直线x=1，x=e2及x轴所围成的图形的面积是S=
dx=lnx
=2．
故选：D．
| 1 |
| x |
| ∫ | e2 1 |
| 1 |
| x |
| | | e2 1 |
故选：D．
点评：本题考查面积的计算，解题的关键是确定曲线交点的坐标，确定被积区间及被积函数，利用定积分表示面积．
练习册系列答案
相关题目
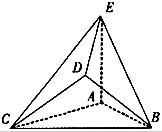在如图所示的几何体中，是边长为2的正三角形，AE＞1，AE⊥平面ABC，平面BCD⊥平面ABC，BD=CD，且BD⊥CD．
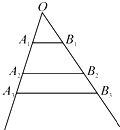如图，互不相同的点A1，A2，…，An，…和B1，B2，…，Bn，…分别在角O的两条边上，所有AnBn相互平行，且所有梯形AnBnBn+1An+1的面积均相等．设OAn=an，若a1=1，a2=2，则a9=
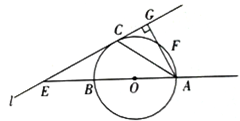已知：直线AB过圆心O，交⊙O于A、B，直线AF交⊙O于A、F（不与B重合），直线l与⊙O相切于C，交AB于E，且与AF垂直，垂足为G，连接AC．下列四个命题中，其中正确的命题的是（ ）
| A、过三点确定一个平面 |
| B、矩形是平面图形 |
| C、四边相等的四边形是平面图形 |
| D、三条直线两两相交则确定一个平面 |