题目内容
设Sn为数列{an}的前n项和,且Sn=(-1)nan-
,n∈N*,则a4a5等于 .
| 1 |
| 2n |
考点:数列的求和
专题:等差数列与等比数列
分析:由于Sn=(-1)nan-
,n∈N*,可得当n≥2时,an=Sn-Sn-1=(-1)nan-
-(-1)n-1an-1+
,分别令n=3,4,5,6即可得出.
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n-1 |
解答:
解:∵Sn=(-1)nan-
,n∈N*,
∴a1=-a1-
,解得a1=-
.
当n≥2时,an=Sn-Sn-1=(-1)nan-
-(-1)n-1an-1+
,
∴2a3=
-a2,a3=-
,a2=
.
2a5=
-a4,a5=-
,a4=
.
∴a4a5=-
.
故答案为:-
.
| 1 |
| 2n |
∴a1=-a1-
| 1 |
| 2 |
| 1 |
| 4 |
当n≥2时,an=Sn-Sn-1=(-1)nan-
| 1 |
| 2n |
| 1 |
| 2n-1 |
∴2a3=
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 4 |
2a5=
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 16 |
∴a4a5=-
| 1 |
| 210 |
故答案为:-
| 1 |
| 210 |
点评:本题考查了递推式的意义,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
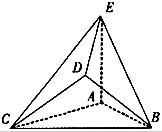 在如图所示的几何体中,是边长为2的正三角形,AE>1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.
在如图所示的几何体中,是边长为2的正三角形,AE>1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD. 如图,在四面体ABCD中,CB=CD,AD⊥BD,点E,F分别是AB,BD的中点
如图,在四面体ABCD中,CB=CD,AD⊥BD,点E,F分别是AB,BD的中点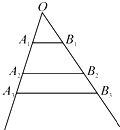 如图,互不相同的点A1,A2,…,An,…和B1,B2,…,Bn,…分别在角O的两条边上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等.设OAn=an,若a1=1,a2=2,则a9=
如图,互不相同的点A1,A2,…,An,…和B1,B2,…,Bn,…分别在角O的两条边上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等.设OAn=an,若a1=1,a2=2,则a9=