题目内容
 已知函数f(x)=ax2-|x|+2a-1(a为实常数).
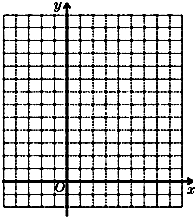
已知函数f(x)=ax2-|x|+2a-1(a为实常数).(Ⅰ)若a=1,作函数f(x)的图象并写出单调区间;
(Ⅱ)当a≥0时,设f(x)在区间[1,2]上的最小值为g(a),求g(a)的表达式;
(Ⅲ)设h(x)=
| f(x) |
| x |
考点:函数图象的作法,函数单调性的判断与证明
专题:函数的性质及应用
分析:(Ⅰ)当a=1时,利用分段函数作函数f(x)的图象并写出单调区间;
(Ⅱ)当a≥0时,根据二次函数的图象和性质即可求g(a)的表达式;
(Ⅲ)利用函数单调性的定义即可得到结论.
(Ⅱ)当a≥0时,根据二次函数的图象和性质即可求g(a)的表达式;
(Ⅲ)利用函数单调性的定义即可得到结论.
解答:
解:(I)当a=1时,f(x)=x2-|x|+1=
,
作图如下

单调减区间:(-∞,-
],[0,
],单调增区间:[-
,0],[
,+∞),
(II)当x∈[1,2]时,f(x)=ax2-x+2a-1.
若a=0,则f(x)=-x-1在区间[1,2]上是减函数,g(a)=f(2)=-3.
若a>0,则f(x)=a(x-
)2+2a-
-1,f(x)图象的对称轴是直线x=
.
当0<
<1,即a>
时,f(x)在区间[1,2]上是增函数,
g(a)=f(1)=3a-2.
当1≤
≤2,即
≤a≤
时,g(a)=f(
)=2a-
-1.
当
>2,即0<a<
时,f(x)在区间[1,2]上是减函数,
g(a)=f(2)=6a-3.
综上可得g(a)=
.
(III)当x∈[1,2]时,h(x)=ax+
-1,在区间[1,2]上任取x1、x2,且x1<x2,
则h(x2)-h(x1)=(ax2+
-1)-(ax1+
-1)=(x2-x1)(a-
)
=(x2-x1)
.…(11分)
因为h(x)在区间[1,2]上是增函数,
所以h(x2)-h(x1)>0.
因为x2-x1>0,x1x2>0,所以ax1x2-(2a-1)>0,
即ax1x2>2a-1.
当a=0时,上面的不等式变为0>-1,即a=0时结论成立.
当a>0时,x1x2>
,由1<x1x2<4,得
≤1,解得0<a≤1.
当a<0时,x1x2<
,由1<x1x2<4,得
≥4,解得-
≤a<0.
所以实数a的取值范围为[-
,1].
|
作图如下

单调减区间:(-∞,-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(II)当x∈[1,2]时,f(x)=ax2-x+2a-1.
若a=0,则f(x)=-x-1在区间[1,2]上是减函数,g(a)=f(2)=-3.
若a>0,则f(x)=a(x-
| 1 |
| 2a |
| 1 |
| 4a |
| 1 |
| 2a |
当0<
| 1 |
| 2a |
| 1 |
| 2 |
g(a)=f(1)=3a-2.
当1≤
| 1 |
| 2a |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2a |
| 1 |
| 4a |
当
| 1 |
| 2a |
| 1 |
| 4 |
g(a)=f(2)=6a-3.
综上可得g(a)=
|
(III)当x∈[1,2]时,h(x)=ax+
| 2a-1 |
| x |
则h(x2)-h(x1)=(ax2+
| 2a-1 |
| x2 |
| 2a-1 |
| x1 |
| 2a-1 |
| x1x2 |
=(x2-x1)
| ax1x2-(2a-1) |
| x1x2 |
因为h(x)在区间[1,2]上是增函数,
所以h(x2)-h(x1)>0.
因为x2-x1>0,x1x2>0,所以ax1x2-(2a-1)>0,
即ax1x2>2a-1.
当a=0时,上面的不等式变为0>-1,即a=0时结论成立.
当a>0时,x1x2>
| 2a-1 |
| a |
| 2a-1 |
| a |
当a<0时,x1x2<
| 2a-1 |
| a |
| 2a-1 |
| a |
| 1 |
| 2 |
所以实数a的取值范围为[-
| 1 |
| 2 |
点评:本题主要考查函数单调性的判断和证明,综合考查函数的性质的应用.

练习册系列答案
相关题目
函数f(x)=lnx+
-1的零点个数为( )
| 1 |
| x |
| A、0 | B、1 | C、2 | D、3 |
下列四个函数中,在(0,+∞)上为增函数的是( )
| A、f(x)=3-x | ||
| B、f(x)=x2-3x | ||
| C、f(x)=-x2 | ||
D、f(x)=-
|
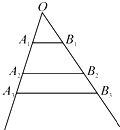 如图,互不相同的点A1,A2,…,An,…和B1,B2,…,Bn,…分别在角O的两条边上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等.设OAn=an,若a1=1,a2=2,则a9=
如图,互不相同的点A1,A2,…,An,…和B1,B2,…,Bn,…分别在角O的两条边上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等.设OAn=an,若a1=1,a2=2,则a9=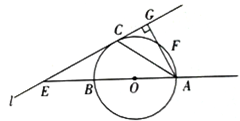 已知:直线AB过圆心O,交⊙O于A、B,直线AF交⊙O于A、F(不与B重合),直线l与⊙O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.
已知:直线AB过圆心O,交⊙O于A、B,直线AF交⊙O于A、F(不与B重合),直线l与⊙O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.