题目内容
14.在△ABC中,角A,B,C的对边分别为a,b,c,若3acosC+b=0,则tanB的最大值是$\frac{3}{4}$.分析 利用正弦定理、诱导公式化简所给的条件求得 tanC=-4tanA,且tanA>0,再利用两角和的正切公式,基本不等式,求得tanB的最大值.
解答 解:在△ABC中,∵3acosC+b=0,∴C为钝角,利用正弦定理可得 3sinAcosC+sin(A+C)=0,
即3sinAcosC+sinAcosC+cosAsinC=0,∴4sinAcosC=-cosAsinC,
即 tanC=-4tanA,∴tanA>0,
则tanB=-tan(A+C)=-$\frac{tanA+tanC}{1-tanAtanC}$=$\frac{tanA+tanC}{tanAtanC-1}$=$\frac{-3tanA}{-{4tan}^{2}A-1}$=$\frac{3}{4tanA+\frac{1}{tanA}}$≤$\frac{3}{2\sqrt{4}}$=$\frac{3}{4}$,
当且仅当tanA=$\frac{1}{2}$时,取等号,故tanB的最大值是$\frac{3}{4}$,
故答案为:$\frac{3}{4}$.
点评 本题主要考查正弦定理、诱导公式、两角和的正切公式的应用,基本不等式,属于中档题.

练习册系列答案
相关题目
2.已知i是虚数单位,复数$z=\frac{3+i}{1+i}$对应的点在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
19.已知集合A={x|x2-1<0},B={x|x>0},则集合(∁RA)∪B=( )
| A. | (0,1] | B. | [1,+∞) | C. | (-∞,-1]∪[1,+∞) | D. | (-∞,-1]∪(0,+∞) |
3.若复数z满足(1+i)z=2-i,则复数z在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.i为虚数单位,复数$z=\frac{i-1}{i+1}$的虚部为( )
| A. | 1 | B. | 0 | C. | i | D. | 以上都不对 |
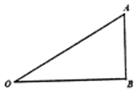 如图,某儿童公园设计一个直角三角形游乐滑梯,AO为滑道,∠OBA为直角,OB=20米,设∠AOB=θrad,一个小朋友从点A沿滑道往下滑,记小朋友下滑的时间为t秒,已知小朋友下滑的长度s与t2和sinθ的积成正比,当$θ=\frac{π}{6}$时,小朋友下滑2秒时的长度恰好为10米.
如图,某儿童公园设计一个直角三角形游乐滑梯,AO为滑道,∠OBA为直角,OB=20米,设∠AOB=θrad,一个小朋友从点A沿滑道往下滑,记小朋友下滑的时间为t秒,已知小朋友下滑的长度s与t2和sinθ的积成正比,当$θ=\frac{π}{6}$时,小朋友下滑2秒时的长度恰好为10米.