题目内容
9.2016年某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计60吨厨余垃圾,假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱和“其他垃圾”箱的投放量分别为x,y,z,其中x>0,x+y+z=60,则数据x,y,z的标准差的最大值为20$\sqrt{2}$.(注:方差${s^2}=\frac{1}{n}[{{{({{x_1}-\overline x})}^2}+{{({{x_2}-\overline x})}^2}+…+{{({{x_n}-\overline x})}^2}}]$,其中$\overline x$为x1,x2,…,xn的平均数)
分析 计算方差可得s2=$\frac{1}{3}$[(x-20)2+(y-20)2+(z-20)2]=$\frac{1}{3}$ (x2+y2+z2-1200),因此有当x=60,y=0,z=0时,有s2=800,进而可得标准差的最大值.
解答 解:由题意可知:∵x+y+z=60,
∴x,y,z的平均数为20
∴s2=$\frac{1}{3}$[(x-20)2+(y-20)2+(z-20)2]=$\frac{1}{3}$ (x2+y2+z2-1200),
∵(x+y+z)2=x2+y2+z2+2xy+2yz+2xz≥x2+y2+z2,
因此有当x=60,y=0,z=0时,
方差最大值s2=800,
此时数据x,y,z的标准差的最大值为20$\sqrt{2}$,
故答案为:20$\sqrt{2}$
点评 本题考查概率知识的运用,考查学生的阅读能力,属于中档题

练习册系列答案
相关题目

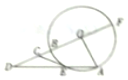 如图,圆O的半径OA与OB相互垂直,E为圆O上一点,直线OB与圆O交于另一点F,与直线AE交于点D,过点E的切线CE交线段于点C,求证:CD2=CB•CF.
如图,圆O的半径OA与OB相互垂直,E为圆O上一点,直线OB与圆O交于另一点F,与直线AE交于点D,过点E的切线CE交线段于点C,求证:CD2=CB•CF.