题目内容
6.分别从集合M{1,2,3}和集合N={4,5,6}中各取一个数,则这两个数之和为偶数的概率为$\frac{4}{9}$.分析 求出所有基本事件,两数之和为偶数的基本事件,即可求两数之和为偶数的概率.
解答 解:从集合M={1,2,3}和集合N={4,5,6}中各取一个数,基本事件共有3×3=9个,
∵两数之和为偶数,
∴两数中全是偶数或全是奇数,故基本事件有1+5,3+5,2+4,2+6,共有4个,
∴两数之积为偶数的概率是$\frac{4}{9}$
故答案为$\frac{4}{9}$.
点评 本题考查概率的计算,考查学生的计算能力,确定基本事件的个数是关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
16.某机械研究所对新研发的某批次机械元件进行寿命追踪调查,随机抽查的200个机械元件情况如下:
若以频率为概率,现从该批次机械元件随机抽取3个,则至少有2个元件的使用寿命在30天以上的概率为( )
| 使用时间(单位:天) | 10:20 | 21:30 | 31:40 | 41:50 | 51:60 |
| 个数 | 10 | 40 | 80 | 50 | 20 |
| A. | $\frac{13}{16}$ | B. | $\frac{27}{64}$ | C. | $\frac{25}{32}$ | D. | $\frac{27}{32}$ |
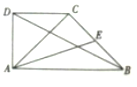 如图,在直角梯形ABCD中,已知AB∥DC,AB⊥AD,AB=2,AD=1,E为BC的中点,若$\overrightarrow{AB}•\overrightarrow{AC}=2$,则$\overrightarrow{AE}•\overrightarrow{BD}$的值为-$\frac{5}{2}$.
如图,在直角梯形ABCD中,已知AB∥DC,AB⊥AD,AB=2,AD=1,E为BC的中点,若$\overrightarrow{AB}•\overrightarrow{AC}=2$,则$\overrightarrow{AE}•\overrightarrow{BD}$的值为-$\frac{5}{2}$.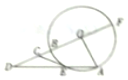 如图,圆O的半径OA与OB相互垂直,E为圆O上一点,直线OB与圆O交于另一点F,与直线AE交于点D,过点E的切线CE交线段于点C,求证:CD2=CB•CF.
如图,圆O的半径OA与OB相互垂直,E为圆O上一点,直线OB与圆O交于另一点F,与直线AE交于点D,过点E的切线CE交线段于点C,求证:CD2=CB•CF.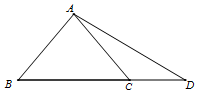 如图,△ABC是等腰直角三角形,∠bac=90°,点D在边BC的延长线上,且BC=2CD,$AD=\sqrt{5}$.
如图,△ABC是等腰直角三角形,∠bac=90°,点D在边BC的延长线上,且BC=2CD,$AD=\sqrt{5}$.