题目内容
5.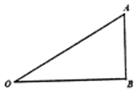 如图,某儿童公园设计一个直角三角形游乐滑梯,AO为滑道,∠OBA为直角,OB=20米,设∠AOB=θrad,一个小朋友从点A沿滑道往下滑,记小朋友下滑的时间为t秒,已知小朋友下滑的长度s与t2和sinθ的积成正比,当$θ=\frac{π}{6}$时,小朋友下滑2秒时的长度恰好为10米.
如图,某儿童公园设计一个直角三角形游乐滑梯,AO为滑道,∠OBA为直角,OB=20米,设∠AOB=θrad,一个小朋友从点A沿滑道往下滑,记小朋友下滑的时间为t秒,已知小朋友下滑的长度s与t2和sinθ的积成正比,当$θ=\frac{π}{6}$时,小朋友下滑2秒时的长度恰好为10米.(1)求s关于时间t的函数的表达式;
(2)请确定θ的值,使小朋友从点A滑到O所需的时间最短.
分析 (1)由题意,设出设S=kt2sinθ的表达式,当$θ=\frac{π}{6}$时,S=10,求解k,可得s关于时间t的函数的表达式;
(2)把OA用θ表示出来,建立关系,化简,利用三角函数的有界限求解即可.
解答 解:(1)由题意,设S=kt2sinθ,t>0,
当$θ=\frac{π}{6}$时,S=10,
∴$10=k×{2^2}sin\frac{π}{6}$,
解得:k=5,
∴故得S关于时间t的函数的表达式;S=5t2sinθ,t>0;
(2)由题意,∠OBA为直角,∠AOB=θrad,
可得:$OA=\frac{20}{cosθ}$,
∴$\frac{20}{cosθ}=5{t^2}sinθ$,
化简可得:$t=\sqrt{\frac{4}{sinθcosθ}}=\frac{{2\sqrt{2}}}{{\sqrt{sin2θ}}}$,
∴当$θ=\frac{π}{4}$时,时间t最短.
点评 本题考查了三角函数的在实际生活中的运用能力和计算能力.属于基础题

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
16.某机械研究所对新研发的某批次机械元件进行寿命追踪调查,随机抽查的200个机械元件情况如下:
若以频率为概率,现从该批次机械元件随机抽取3个,则至少有2个元件的使用寿命在30天以上的概率为( )
| 使用时间(单位:天) | 10:20 | 21:30 | 31:40 | 41:50 | 51:60 |
| 个数 | 10 | 40 | 80 | 50 | 20 |
| A. | $\frac{13}{16}$ | B. | $\frac{27}{64}$ | C. | $\frac{25}{32}$ | D. | $\frac{27}{32}$ |
