题目内容
3．若复数z满足（1+i）z=2-i，则复数z在复平面内对应的点在（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 利用复数的运算法则、几何意义即可得出．
解答 解：复数z满足（1+i）z=2-i，∴（1-i）（1+i）z=（1-i）（2-i），∴2z=1-3i，∴z=$\frac{1}{2}-\frac{3}{2}$i．
则复数z在复平面内对应的点$（\frac{1}{2}，-\frac{3}{2}）$在第四象限．
故选：D．
点评 本题考查了复数的运算法则、几何意义，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
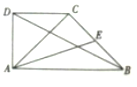如图，在直角梯形ABCD中，已知AB∥DC，AB⊥AD，AB=2，AD=1，E为BC的中点，若$\overrightarrow{AB}•\overrightarrow{AC}=2$，则$\overrightarrow{AE}•\overrightarrow{BD}$的值为-$\frac{5}{2}$．
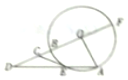如图，圆O的半径OA与OB相互垂直，E为圆O上一点，直线OB与圆O交于另一点F，与直线AE交于点D，过点E的切线CE交线段于点C，求证：CD2=CB•CF．
8．已知实数x，y满足|x|≤y+1，且-1≤y≤1，则z=2x+y的最大值（ ）
| A． | 2 | B． | 4 | C． | 5 | D． | 6 |
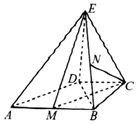如图，在直角梯形ABCD中，AB∥CD，AB=2CD，∠BCD=90．，BC=CD，AE=BE，ED⊥平面ABCD．