题目内容
已知a,b为实数,则“2a>2b”是“a2>b2”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据不等式的性质,利用充分条件和必要条件的定义即可得到结论.
解答:
解:若2a>2b,则a>b,当a=1,b=-1时,a2>b2不成立,充分性不成立,
当a=-1,b=0时,满足a2>b2成立,但2a>2b不成立,即必要性不成立,
故“2a>2b”是“a2>b2”的既不充分也不必要条件,
故选:D.
当a=-1,b=0时,满足a2>b2成立,但2a>2b不成立,即必要性不成立,
故“2a>2b”是“a2>b2”的既不充分也不必要条件,
故选:D.
点评:本题主要考查充分条件和必要条件的判定,利用不等式之间的关系是解决本题的关键,比较基础.

练习册系列答案
 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
在梯形ABCD中,AB∥DC,AD⊥AB,AB=2AD=2DC=4,点N是CD边上一动点,则
•
的最大值为( )
| AN |
| AB |
A、4
| ||
| B、8 | ||
C、8
| ||
| D、16 |
已知集合A={1,2,4},B={y|y=log2x,x∈A},则A∪B=( )
| A、{0,1,2} |
| B、{1,2} |
| C、{0,1,2,4} |
| D、{0,1,4} |
若l,m为空间两条不同的直线,α,β为空间两个不同的平面,则l丄α的一个充分条件是( )
| A、l∥β且α丄β |
| B、l?β且α丄β |
| C、l丄β且α∥β |
| D、l丄m且m∥α |
设函数f(x)=|sin(2x+
)|,则下列关于函数f(x)的说法中正确的是( )
| π |
| 3 |
A、f(x)图象关于直线x=
| ||||
| B、f(x)的最小正周期为π | ||||
C、f(x)图象关于点(-
| ||||
D、f(x)在区间[
|
函数y=x3-3x+1在[-2,1]上的最大值为( )
| A、3 | B、4 | C、5 | D、6 |
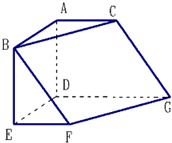 在图的几何体中,面ABC∥面DEFG,∠BAC=∠EDG=120°,四边形 ABED 是矩形,四边形ADGC 是直角梯形,∠ADG=90°,四边形 DEFG 是梯形,EF∥DG,AB=AC=AD=EF=1,DG=2.
在图的几何体中,面ABC∥面DEFG,∠BAC=∠EDG=120°,四边形 ABED 是矩形,四边形ADGC 是直角梯形,∠ADG=90°,四边形 DEFG 是梯形,EF∥DG,AB=AC=AD=EF=1,DG=2.