题目内容
在梯形ABCD中，AB∥DC，AD⊥AB，AB=2AD=2DC=4，点N是CD边上一动点，则
•
的最大值为（ ）
| AN |
| AB |
A、4
| ||
| B、8 | ||
C、8
| ||
| D、16 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：如图所示，建立直角坐标系．由已知可设N（x，2），（0≤x≤2）．得到
=（4，0），
=（x，2）．再利用数量积运算和一次函数的单调性即可得出．
| AB |
| AN |
解答：
解：如图所示，
∵在梯形ABCD中，AB∥DC，AD⊥AB，AB=2AD=2DC=4，
∴可设N（x，2），（0≤x≤2）．
∴
=（4，0），
=（x，2）．
∴
•
=4x≤8，当x=2时取等号．
∴
•
的最大值为8．
故想：B．
∵在梯形ABCD中，AB∥DC，AD⊥AB，AB=2AD=2DC=4，
∴可设N（x，2），（0≤x≤2）．
∴
| AB |
| AN |
∴
| AN |
| AB |
∴
| AN |
| AB |
故想：B．
点评：本题考查了向量的数量积运算和一次函数的单调性，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
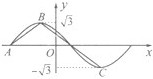如图为函数f（x）=| 3 |
| AB |
| BC |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|
设
＜a＜π，sinα=
，则
的值为（ ）
| π |
| 2 |
| 4 |
| 5 |
| sin2α+sin2α |
| cos2α+cos2α |
| A、8 | B、10 | C、-4 | D、-20 |
数列{an}的前n项和sn，若a1=1，an=
，Sn=124，则n=（ ）
|
| A、8 | B、9 | C、10 | D、11 |
某地区对两所高中学校进行学生体质状况抽测，甲校有学生800人，乙校有学生500人，现用分层抽样的方法在这1300名学生中抽取一个样本．已知在甲校抽取了48人，则在乙校应抽取学生人数为（ ）
| A、48 | B、36 | C、30 | D、24 |
已知a，b为实数，则“2a＞2b”是“a2＞b2”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既充分也不必要条件 |