题目内容
若l,m为空间两条不同的直线,α,β为空间两个不同的平面,则l丄α的一个充分条件是( )
| A、l∥β且α丄β |
| B、l?β且α丄β |
| C、l丄β且α∥β |
| D、l丄m且m∥α |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据线面垂直的定义和判定定理,利用充分条件和必要条件的定义进行判断即可得到结论.
解答:
解:A.若l∥β且α丄β,则l丄α不一定成立,
B.若l?β且α丄β,则l丄α不一定成立
C.若l丄β且α∥β,则l丄α一定成立
D.若l丄m且m∥α,则l丄α不一定成立
故选:C.
B.若l?β且α丄β,则l丄α不一定成立
C.若l丄β且α∥β,则l丄α一定成立
D.若l丄m且m∥α,则l丄α不一定成立
故选:C.
点评:本题主要考查充分条件和必要条件的判定,利用线面垂直的定义和判定定理是解决本题的关键,比较基础.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
设
<a<π,sinα=
,则
的值为( )
| π |
| 2 |
| 4 |
| 5 |
| sin2α+sin2α |
| cos2α+cos2α |
| A、8 | B、10 | C、-4 | D、-20 |
某地区对两所高中学校进行学生体质状况抽测,甲校有学生800人,乙校有学生500人,现用分层抽样的方法在这1300名学生中抽取一个样本.已知在甲校抽取了48人,则在乙校应抽取学生人数为( )
| A、48 | B、36 | C、30 | D、24 |
已知a,b为实数,则“2a>2b”是“a2>b2”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既充分也不必要条件 |
要得到函数y=cos(2x-
)的图象,只需将函数y=sin(2x)的图象( )
| π |
| 3 |
A、左移
| ||
B、右移
| ||
C、左移
| ||
D、右移
|
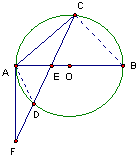 如图,已知AB是⊙O的直径,弦CD与AB交于点E,过点A作圆的切线与CD的延长线交于点F,如果DE=
如图,已知AB是⊙O的直径,弦CD与AB交于点E,过点A作圆的切线与CD的延长线交于点F,如果DE=