题目内容
已知函数f(x)=lnx-x,若f(x)-m+1≤0恒成立,求m的取值范围. .
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:把f(x)=lnx-x代入f(x)-m+1≤0,由f(x)-m+1≤0恒成立得到m≥lnx-x+1恒成立,构造函数g(x)=lnx-x+1(x>0).利用导数求其最大值得答案.
解答:
解:∵f(x)=lnx-x,
则f(x)-m+1≤0恒成立等价于m≥lnx-x+1.
令g(x)=lnx-x+1(x>0).
则g′(x)=
-1=
.
当x∈(0,1)时,g′(x)>0,函数g(x)为增函数;
当x∈(1,+∞)时,g′(x)<0,函数g(x)为减函数.
∴当x=1时,函数g(x)有极大值,也就是最大值.
∴g(x)max=g(1)=0.
∴m≥0.
故答案为:m≥0.
则f(x)-m+1≤0恒成立等价于m≥lnx-x+1.
令g(x)=lnx-x+1(x>0).
则g′(x)=
| 1 |
| x |
| 1-x |
| x |
当x∈(0,1)时,g′(x)>0,函数g(x)为增函数;
当x∈(1,+∞)时,g′(x)<0,函数g(x)为减函数.
∴当x=1时,函数g(x)有极大值,也就是最大值.
∴g(x)max=g(1)=0.
∴m≥0.
故答案为:m≥0.
点评:本题考查了恒成立问题,考查了利用导数求函数的最值,考查了数学转化思想方法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
等比数列{an}的各项均为正数,且a5a6+a3a8=6,则log3a1+log3a2+…+log3a10=( )
| A、6 |
| B、5 |
| C、4 |
| D、2+log35 |
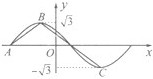 如图为函数f(x)=
如图为函数f(x)=| 3 |
| AB |
| BC |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知a,b为实数,则“2a>2b”是“a2>b2”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既充分也不必要条件 |
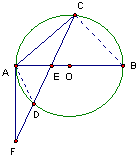 如图,已知AB是⊙O的直径,弦CD与AB交于点E,过点A作圆的切线与CD的延长线交于点F,如果DE=
如图,已知AB是⊙O的直径,弦CD与AB交于点E,过点A作圆的切线与CD的延长线交于点F,如果DE=