题目内容
4．双曲线${x^2}-\frac{y^2}{9}=1$的实轴长为2．分析 根据题意，由双曲线的方程可得a的值，进而由双曲线的实轴公式计算可得答案．
解答 解：双曲线的方程为${x^2}-\frac{y^2}{9}=1$，
其中a=1，
则其实轴长2a=2；
故答案为：2．
点评 本题考查双曲线的几何性质，注意实轴长为2a，需由双曲线的方程求出a的值．
练习册系列答案
相关题目
14．如图，已知$\overrightarrow{AB}=a$，$\overrightarrow{AC}=b$，$\overrightarrow{DC}=3\overrightarrow{BD}$，$\overrightarrow{AE}=2\overrightarrow{EC}$，则$\overrightarrow{DE}$=（ ）
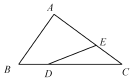
| A． | $\frac{3}{4}b-\frac{1}{3}a$ | B． | $\frac{5}{12}a-\frac{3}{4}b$ | C． | $\frac{3}{4}a-\frac{1}{3}b$ | D． | $\frac{5}{12}b-\frac{3}{4}a$ |
15．某班级为了进行户外拓展游戏，组成红、蓝、黄3个小队．甲、乙两位同学各自等可能地选择其中一个小队，则他们选到同一小队的概率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
19．在复平面内，复数$z=\frac{2i}{1-i}$对应的点的坐标为（ ）
| A． | （1，-1） | B． | （1，1） | C． | （-1，1） | D． | （-1，-1） |
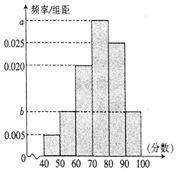某校从高一年级学生中随机抽取40名学生，将他们的期中考试数学成绩（满分100分，成绩均为不低于40分的整数）分成六段：[40，50），[50，60），…，[90，100]后得到如图所示的频率分布直方图，其中前三段的频率成等比数列．