题目内容

19．在复平面内，复数$z=\frac{2i}{1-i}$对应的点的坐标为（　　）
A．（1，-1）B．（1，1）C．（-1，1）D．（-1，-1）

分析 利用复数的运算法则、几何意义即可得出．

解答 解：复数$z=\frac{2i}{1-i}$=$\frac{2i（1+i）}{（1-i）（1+i）}$=i-1对应的点的坐标为（-1，1）．
故选：C．

点评 本题考查了复数的运算法则、几何意义，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
9．已知复数z满足$z=\frac{1+2i}{{{{（1-i）}^2}}}$，则在复平面内复数$\overline z$对应的点为（　　）
A．$（-1，-\frac{1}{2}）$B．$（1，-\frac{1}{2}）$C．$（-\frac{1}{2}，1）$D．$（-\frac{1}{2}，-1）$
10．第31届夏季奥林匹克运动会于2016年8月5日至21日在巴西里约热内卢举行，为了选拔某个项目的奥运会参赛队员，共举行5次达标测试，选手如果通过2次达标测试即可参加里约奥运会，不用参加其余的测试，而每个选手最多只能参加5次测试，假设某个选手每次通过测试的概率都是$\frac{1}{3}$，每次测试通过与是相互独立．规定：若前4次都没有通过测试，则第5次不能参加测试．
（1）求该选手能够参加本届奥运会的概率；
（2）记该选手参加测试的次数为X，求随机变量X的分布列及数学期望E（X）．
7．已知f（x）是R上的奇函数，则“x1+x2=0”是“f（x1）+f（x2）=0”的（　　）
A．充分而不必要条件B．必要而不充分条件
C．充分必要条件D．既不充分也不必要条件
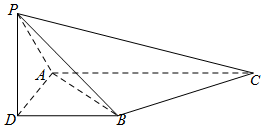14．如图，三棱锥P-ABC，侧棱PA=2，底面三角形ABC为正三角形，边长为2，顶点P在平面ABC上的射影为D，有AD⊥DB，且DB=1．
（Ⅰ）求证：AC∥平面PDB；
（Ⅱ）求二面角P-AB-C的余弦值；
（Ⅲ）线段PC上是否存在点E使得PC⊥平面ABE，如果存在，求$\frac{CE}{CP}$的值；如果不存在，请说明理由．
4．双曲线${x^2}-\frac{y^2}{9}=1$的实轴长为2．
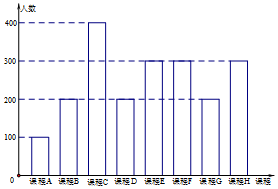11．为了响应教育部颁布的《关于推进中小学生研学旅行的意见》，某校计划开设八门研学旅行课程，并对全校学生的选课意向进行调查（调查要求全员参与，每个学生必须从八门课程中选出唯一一门课程）．本次调查结果如下．图中，课程A，B，C，D，E为人文类课程，课程F，G，H为自然科学类课程．为进一步研究学生选课意向，结合上面图表，采取分层抽样方法从全校抽取1%的学生作为研究样本组（以下简称“组M”）．
（Ⅰ）在“组M”中，选择人文类课程和自然科学类课程的人数各有多少？
（Ⅱ）某地举办自然科学营活动，学校要求：参加活动的学生只能是“组M”中选择F课程或G课程的同学，并且这些同学以自愿报名缴费的方式参加活动．选择F课程的学生中有x人参加科学营活动，每人需缴纳2000元，选择G课程的学生中有y人参加该活动，每人需缴纳1000元．记选择F课程和G课程的学生自愿报名人数的情况为（x，y），参加活动的学生缴纳费用总和为S元．
（ⅰ）当S=4000时，写出（x，y）的所有可能取值；
（ⅱ）若选择G课程的同学都参加科学营活动，求S＞4500元的概率．
8．已知等比数列{an}，且a6+a8=4，则a8（a4+2a6+a8）的值为（　　）
A．2B．4C．8D．16
9．将一条均匀木棍随机折成两段，则其中一段大于另一段三倍的概率为（　　）
A．$\frac{3}{4}$B．$\frac{2}{3}$C．$\frac{1}{2}$D．$\frac{1}{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网