题目内容
（理）若（x+
）n的展开式中前三项的系数成等差数列，则展开式中x6项的系数为（ ）
| 1 |
| 2x |
| A、4 | B、7 | C、8 | D、2 |
考点：二项式系数的性质
专题：二项式定理
分析：利用二项展开式的通项公式求出展开式的通项，求出前三项的系数，列出方程求出n；将n的值代入通项，令x的指数等于6，求出展开式中x6项的系数．
解答：
解：展开式的通项为Tr+1=（
）r
xn-2r，
前三项的系数为1，
，
，
∴n=1+
，
解得n=8．
∴展开式的通项为Tr+1=（
）r
x8-2r，
令8-2r=6得r=1，
∴展开式中x6项的系数：
×
=4，
故选：A．
| 1 |
| 2 |
| C | r n |
前三项的系数为1，
| n |
| 2 |
| n(n-1) |
| 8 |
∴n=1+
| n(n-1) |
| 8 |
解得n=8．
∴展开式的通项为Tr+1=（
| 1 |
| 2 |
| C | r 8 |
令8-2r=6得r=1，
∴展开式中x6项的系数：
| 1 |
| 2 |
| C | 1 8 |
故选：A．
点评：本题考查利用二项展开式的通项公式解决二项展开式的特定项问题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知a、b为空间中不同的直线，α、β、γ为不同的平面，下列命题中正确命题的个数是（ ）
（1）若a∥α，a⊥b，则b⊥α；
（2）α∥β，α⊥γ，则β⊥γ；
（3）若a∥β，b∥β，a，b?α，则α∥β
（4）α⊥β，a⊥β，则a∥α
（1）若a∥α，a⊥b，则b⊥α；
（2）α∥β，α⊥γ，则β⊥γ；
（3）若a∥β，b∥β，a，b?α，则α∥β
（4）α⊥β，a⊥β，则a∥α
| A、0 | B、1 | C、2 | D、3 |
等边△ABC的边长为1，过△ABC的中心O作OP⊥平面ABC，且OP=
| ||
| 3 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
已知定义域为R的函数f（x）满足f（-x）=-f（x+4），且函数f（x）在区间（2，+∞）上单调递增，如果x1＜2＜x2，且x1+x2＜4，则f（x1）+f（x2）的值（ ）
| A、恒小于0 | B、恒大于0 |
| C、可能为0 | D、可正可负 |
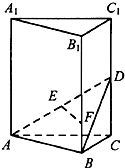如图，在直三棱柱ABC-A1B1C1中，D、E分别为CC1、AD的中点，F为BB1上的点，且B1F=3BF