题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c.已知a=3,b=8,C=
,则c= .
| π |
| 3 |
考点:余弦定理
专题:三角函数的求值,解三角形
分析:由a,b,cosC的值,利用余弦定理即可求出c的值.
解答:
解:∵a=3,b=8,C=
,
∴由余弦定理得:c2=a2+b2-2abcosC=9+64-24=49,
则c=7.
故答案为:7
| π |
| 3 |
∴由余弦定理得:c2=a2+b2-2abcosC=9+64-24=49,
则c=7.
故答案为:7
点评:此题考查了余弦定理,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目
冬天是感冒传播的高发季节,连续6周中,每周患病发烧的人数如表所示,图为统计六周发烧人数的程序框图,则图中判断框,执行框应填( )

| 周次 | 1 | 2 | 3 | 4 | 5 | 6 |
| 发烧人数 | a1 | a2 | a3 | a4 | a5 | a6 |
| A、i<6;s=s+ai |
| B、i≤6;s=s+i |
| C、i≤6;s=s+ai |
| D、i>6;s=a1+a2+…+ai |
(理)若(x+
)n的展开式中前三项的系数成等差数列,则展开式中x6项的系数为( )
| 1 |
| 2x |
| A、4 | B、7 | C、8 | D、2 |

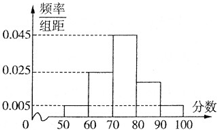 某学校举行课外综合知识比赛,随机抽取400名同学的成绩,成绩全部在50分至100分之间,将成绩按如下方式分成5组:第一组,成绩大于等于50分且小于60分;第二组,成绩大于等于60分且小于70分…第五组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图.则400名同学中成绩优秀(大于等于80分)的学生有
某学校举行课外综合知识比赛,随机抽取400名同学的成绩,成绩全部在50分至100分之间,将成绩按如下方式分成5组:第一组,成绩大于等于50分且小于60分;第二组,成绩大于等于60分且小于70分…第五组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图.则400名同学中成绩优秀(大于等于80分)的学生有