题目内容
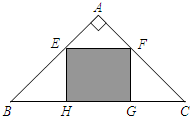如图，有一块等腰直角三角形ABC的空地，要在这块空地上开辟一个内接矩形EFGH的绿地，已知AB⊥AC，AB=4，绿地面积最大值为（ ）| A、6 | ||
B、4
| ||
| C、4 | ||
D、2
|
考点：函数的最值及其几何意义
专题：函数的性质及应用
分析：经分析可知，△AEF，△FGC都是等腰直角三角形，可设AF=x，则FC=4-x，则EF，FG都可用x表示出来，所以矩形EFGH的面积S就用x表示出来了，然后只需出求函数S=
f（x）的最值即可．
f（x）的最值即可．
解答：
解：如图，设AF=x，则0＜x＜4，∴FC=4-x，
则在等腰直角△AEF中，EF=
x，在等腰直角△FGC中，FG=
(4-x)，
∴矩形EFGH的面积S=EF•FG=
x•
(4-x)=-x2+4x，（0＜x＜4）
所以S=-（x-2）2+4，（0＜x＜4）
∴x=2时Smax=4．
故选：C．
如图，设AF=x，则0＜x＜4，∴FC=4-x，则在等腰直角△AEF中，EF=
| 2 |
| ||
| 2 |
∴矩形EFGH的面积S=EF•FG=
| 2 |
| ||
| 2 |
所以S=-（x-2）2+4，（0＜x＜4）
∴x=2时Smax=4．
故选：C．
点评：这是一个利用二次函数解决实际问题的题目，首先要选取自变量AF=x，然后找到所求面积S与自变量x之间的等量关系，将面积用S表示出来，然后再利用函数的性质求其最值，要注意自变量的取值范围，即函数的定义域．
练习册系列答案
相关题目
已知x∈R，则“x2-3x＜0”是“（x-1）（x-2）≤0成立”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
用反证法证明命题：若a+b+c为偶数，则“自然a、b、c恰有一个偶数”时正确反设为（ ）
| A、a、b、c都是奇数 |
| B、a、b、c都是偶数 |
| C、a、b、c中至少有两个偶数 |
| D、a、b、c中或都是奇数或至少有两个偶数 |
已知函数f（x）=|x2-4|-3x+m恰有两个不同的零点，则实数m的取值范围是（ ）
A、（-6，6）∪（
| ||
B、（
| ||
C、（-∞，-
| ||
D、（-
|
直线y=x+2与曲线
-
=1的交点个数为（ ）
| y2 |
| 2 |
| x|x| |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
设直线l经过点P（2，1），且A（0，4）、B（4，8）两点到直线l的距离相等，则直线l的方程是（ ）
| A、x-y-1=0 |
| B、x-y-1=0或x-y-4=0 |
| C、x+y-3=0 |
| D、x-y-1=0或x=2 |
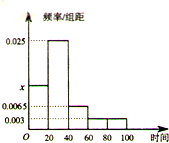某学校随机抽取部分新生调查其上学所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中，上学所需时间的范围是[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100）．