题目内容
已知函数f(x)=|x2-4|-3x+m恰有两个不同的零点,则实数m的取值范围是( )
A、(-6,6)∪(
| ||
B、(
| ||
C、(-∞,-
| ||
D、(-
|
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:由f(x)=0,得m=3x-|x2-4|,作出函数y=g(x)=3x-|x2-4|图象,利用数形结合即可得到结论.
解答:
解:由f(x)=0,得m=3x-|x2-4|,
设g(x)=3x-|x2-4|,
当x≥2或x≤-2时,g(x)=3x-|x2-4|=g(x)=3x-x2+4=-(x-
)2+
,
当-2<x<2时,g(x)=3x-|x2-4|=g(x)=3x+x2-4=(x+
)2-
,
作出y=g(x)=3x-|x2-4|图象如图:
要使函数f(x)=|x2-4|-3x+m恰有两个不同的零点,
则m<-
或-6<m<6,
即m∈(-∞,-
)∪(-6,6),
故选:C
设g(x)=3x-|x2-4|,

当x≥2或x≤-2时,g(x)=3x-|x2-4|=g(x)=3x-x2+4=-(x-
| 3 |
| 2 |
| 25 |
| 4 |
当-2<x<2时,g(x)=3x-|x2-4|=g(x)=3x+x2-4=(x+
| 3 |
| 2 |
| 25 |
| 4 |
作出y=g(x)=3x-|x2-4|图象如图:
要使函数f(x)=|x2-4|-3x+m恰有两个不同的零点,
则m<-
| 25 |
| 4 |
即m∈(-∞,-
| 25 |
| 4 |
故选:C
点评:本题主要考查根的存在性的应用,利用一元二次函数的图象和性质,以及数形结合是解决本题的关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
若sinθ=
,θ∈R,则方程的解集为( )
| ||
| 2 |
A、{θ|θ=
| ||||
B、{θ|θ=
| ||||
C、{θ|θ=
| ||||
D、{θ|θ=
|
在△ABC中,若sinA>sinB,则( )
| A、A=B | B、A<B |
| C、A>B | D、不确定 |
数列1,3,6,10,x,21,…中,x的值是 ( )
| A、12 | B、13 | C、15 | D、16 |
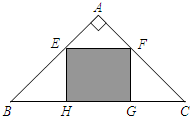 如图,有一块等腰直角三角形ABC的空地,要在这块空地上开辟一个内接矩形EFGH的绿地,已知AB⊥AC,AB=4,绿地面积最大值为( )
如图,有一块等腰直角三角形ABC的空地,要在这块空地上开辟一个内接矩形EFGH的绿地,已知AB⊥AC,AB=4,绿地面积最大值为( )