题目内容
直线y=x+2与曲线
-
=1的交点个数为( )
| y2 |
| 2 |
| x|x| |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
考点:椭圆的简单性质,双曲线的简单性质
专题:数形结合,圆锥曲线的定义、性质与方程
分析:作出曲线
-
=1的图象,利用y=x+2是y2+x2=2的切线,渐近线方程为y=±x,即可得出结论.
| y2 |
| 2 |
| x|x| |
| 2 |
解答:
 解:当x≥0时,曲线方程为
解:当x≥0时,曲线方程为
-
=1,图形为双曲线在y轴的右半部分;
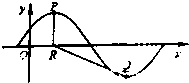
当x<0时,曲线方程为y2+x2=2,图形为圆在y轴的左半部分;如图所示,
∵y=x+2是y2+x2=2的切线,渐近线方程为y=±x
∴直线y=x+2与曲线
-
=1的交点个数为1.
故选:B.
 解:当x≥0时,曲线方程为
解:当x≥0时,曲线方程为| y2 |
| 2 |
| x2 |
| 2 |
当x<0时,曲线方程为y2+x2=2,图形为圆在y轴的左半部分;如图所示,
∵y=x+2是y2+x2=2的切线,渐近线方程为y=±x
∴直线y=x+2与曲线
| y2 |
| 2 |
| x|x| |
| 2 |
故选:B.
点评:本题考查直线与圆锥曲线的关系,题目中所给的曲线是部分双曲线的椭圆组成的图形,只要注意分类讨论就可以得出结论,本题是一个基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图为某算法的程序框图,则程序运行后输出的结果是( )

| A、3 | B、4 | C、5 | D、6 |
已知双曲线的一个焦点坐标为(
,0),且经过点(-5,2),则双曲线的标准方程为( )
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
数列1,3,6,10,x,21,…中,x的值是 ( )
| A、12 | B、13 | C、15 | D、16 |
 已知函数f(x)=Asin(
已知函数f(x)=Asin(| π |
| 3 |
| π |
| 2 |
| 2π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
已知点D是△ABC的边BC上的中点,且|
|=4,|
|=2,则
•
=( )
| AC |
| AB |
| AD |
| BC |
| A、2 | ||
| B、4 | ||
| C、6 | ||
D、2
|
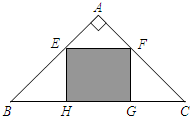 如图,有一块等腰直角三角形ABC的空地,要在这块空地上开辟一个内接矩形EFGH的绿地,已知AB⊥AC,AB=4,绿地面积最大值为( )
如图,有一块等腰直角三角形ABC的空地,要在这块空地上开辟一个内接矩形EFGH的绿地,已知AB⊥AC,AB=4,绿地面积最大值为( )