题目内容
设直线l经过点P（2，1），且A（0，4）、B（4，8）两点到直线l的距离相等，则直线l的方程是（ ）
| A、x-y-1=0 |
| B、x-y-1=0或x-y-4=0 |
| C、x+y-3=0 |
| D、x-y-1=0或x=2 |
考点：点到直线的距离公式
专题：直线与圆
分析：对直线l的斜率分类讨论，再利用斜率计算公式和点斜式即可得出．
解答：
解：当直线l的斜率不存在时，直线l的方程为：x=2，此时A（0，4）、B（4，8）两点到直线l的距离相等，因此x=2满足条件；
当直线l的斜率存在时，则kl=kAB=
=1，
∴直线l的方程为：y-1=1×（x-2），化为x-y-1=0．
综上可得直线l的方程为：x-y-1=0或x=2．
故选：D．
当直线l的斜率存在时，则kl=kAB=
| 8-4 |
| 4-0 |
∴直线l的方程为：y-1=1×（x-2），化为x-y-1=0．
综上可得直线l的方程为：x-y-1=0或x=2．
故选：D．
点评：本题考查了分类讨论、斜率计算公式和点斜式，属于基础题．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
在下列函数中，最小值为2的是（ ）
A、y=x+
| ||||
B、y=sinx+
| ||||
C、y=lgx+
| ||||
| D、y=3x+3-x |
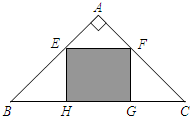如图，有一块等腰直角三角形ABC的空地，要在这块空地上开辟一个内接矩形EFGH的绿地，已知AB⊥AC，AB=4，绿地面积最大值为（ ）