题目内容
在研究色盲与性别的关系调查中,调查了男性480人,其中有38人患色盲,调查的520个女性中6人患色盲,
(1)根据以上的数据建立一个2×2的列联表;
(2)能否有99.9%的把握认为“性别与患色盲有关系”?
(1)根据以上的数据建立一个2×2的列联表;
(2)能否有99.9%的把握认为“性别与患色盲有关系”?
考点:独立性检验的应用
专题:计算题,概率与统计
分析:(1)根据调查了男性480人,其中有38人患色盲,调查的520名女性中有6人患色盲,列出列联表;
(2)代入公式计算得出K2值,结合临界值,即可求得结论.
(2)代入公式计算得出K2值,结合临界值,即可求得结论.
解答:
解:(1)
(2)假设H:“性别与患色盲没有关系”
先算出K 的观测值:K2=
≈27.139.
由于27.139>10.828,
∴有99.9%的把握认为色盲与性别是有关的,
即是H 成立的概率不超过0.001,
即“性别与患色盲有关系”,则出错的概率为0.001.
| 患色盲 | 不患色盲 | 总计 | |
| 男 | 38 | 442 | 480 |
| 女 | 6 | 514 | 520 |
| 总计 | 44 | 956 | 1000 |
先算出K 的观测值:K2=
| 1000×(442×6-38×514)2 |
| 44×956×480×520 |
由于27.139>10.828,
∴有99.9%的把握认为色盲与性别是有关的,
即是H 成立的概率不超过0.001,
即“性别与患色盲有关系”,则出错的概率为0.001.
点评:本题考查独立性检验知识,考查学生的计算能力,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
数列1,3,6,10,x,21,…中,x的值是 ( )
| A、12 | B、13 | C、15 | D、16 |
已知点D是△ABC的边BC上的中点,且|
|=4,|
|=2,则
•
=( )
| AC |
| AB |
| AD |
| BC |
| A、2 | ||
| B、4 | ||
| C、6 | ||
D、2
|
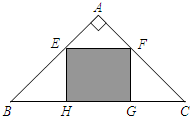 如图,有一块等腰直角三角形ABC的空地,要在这块空地上开辟一个内接矩形EFGH的绿地,已知AB⊥AC,AB=4,绿地面积最大值为( )
如图,有一块等腰直角三角形ABC的空地,要在这块空地上开辟一个内接矩形EFGH的绿地,已知AB⊥AC,AB=4,绿地面积最大值为( )