题目内容
某次文艺晚会上共演出8个节目,其中2个歌曲,3个舞蹈,3个曲艺节目,求分别满足下列条件的节目编排方法有多少种?
(1)一个歌曲节目开头,另一个放在最后压台;
(2)2个歌曲节目互不相邻.
(1)一个歌曲节目开头,另一个放在最后压台;
(2)2个歌曲节目互不相邻.
考点:计数原理的应用
专题:应用题,排列组合
分析:(1)先排歌曲节目,再排其他节目,利用乘法原理,即可得出结论;
(2)先排3个舞蹈,3个曲艺节目,再利用插空法排唱歌,即可得到结论.
(2)先排3个舞蹈,3个曲艺节目,再利用插空法排唱歌,即可得到结论.
解答:
解:(1)先排歌曲节目有
种排法,再排其他节目有
种排法,所以共有
=1440种排法.
(2)先排3个舞蹈节目,3个曲艺节目,有
种排法,再从其中7个空(包括两端)中选2个排歌曲节目,有
种插入方法,所以共有
=30240种排法.
| A | 2 2 |
| A | 6 6 |
| A | 2 2 |
| A | 6 6 |
(2)先排3个舞蹈节目,3个曲艺节目,有
| A | 6 6 |
| A | 2 7 |
| A | 6 6 |
| A | 2 7 |
点评:本题考查排列组合知识,考查学生利用数学知识解决实际问题的能力,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
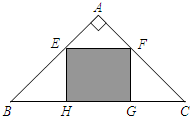 如图,有一块等腰直角三角形ABC的空地,要在这块空地上开辟一个内接矩形EFGH的绿地,已知AB⊥AC,AB=4,绿地面积最大值为( )
如图,有一块等腰直角三角形ABC的空地,要在这块空地上开辟一个内接矩形EFGH的绿地,已知AB⊥AC,AB=4,绿地面积最大值为( )