题目内容
20．
如图，网格纸上小正方形的边长为1，粗线画出的一个三棱锥的三视图，则该三棱锥的表面积为（ ）| A． | $\frac{{15+\sqrt{17}}}{2}$ | B． | $\frac{{13+\sqrt{17}}}{2}$ | C． | $\frac{{11+\sqrt{17}}}{2}$ | D． | $\frac{{9+\sqrt{17}}}{2}$ |
分析 以正方体为载体作出三棱锥的直观图，求出棱锥的各棱长，利用余弦定理求出各面面积．
解答 
解：设正方体ABCD-A1B1C1D1棱长为2，M，N分别是A1B1，A1D1的中点，
则三棱锥C-AMN为所求几何体．
由图可知AM=AN=$\sqrt{5}$，MN=$\sqrt{2}$，AC=2$\sqrt{2}$，CM=CN=3，
由余弦定理得cos∠MAN=$\frac{5+5-2}{2•\sqrt{5}•\sqrt{5}}$=$\frac{4}{5}$，∴sin∠MAN=$\frac{3}{5}$，
∴S△MAN=$\frac{1}{2}×\sqrt{5}×\sqrt{5}×\frac{3}{5}$=$\frac{3}{2}$，
同理可得S△MCN=$\frac{\sqrt{17}}{2}$，SMAC=S△NAC=3，
∴棱锥的表面积S=$\frac{3}{2}+\frac{\sqrt{17}}{2}+3×2$=$\frac{15+\sqrt{17}}{2}$．
故选：A．
点评 本题考查了棱锥的结构特征和三视图，作出棱锥的直观图是解题关键，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
将集合{2t+2s|0≤s＜t，且s，t∈Z}中所有的数按照上小下大，左小右大的原则写成如图的三角形数表：则该数表中，从小到大第50个数为1040．
15．如图是2017年第一季度五省GDP情况图，则下列陈述正确的是（ ）
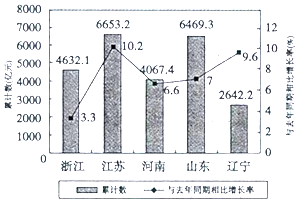
①2017年第一季度GDP总量和增速均居同一位的省只有1个；
②与去年同期相比，2017年第一季度五个省的GDP总量均实现了增长；
③去年同期的GDP总量前三位是江苏、山东、浙江；
④2016年同期浙江的GDP总量也是第三位．
①2017年第一季度GDP总量和增速均居同一位的省只有1个；
②与去年同期相比，2017年第一季度五个省的GDP总量均实现了增长；
③去年同期的GDP总量前三位是江苏、山东、浙江；
④2016年同期浙江的GDP总量也是第三位．
| A． | ①② | B． | ②③④ | C． | ②④ | D． | ①③④ |
9．某公司出售某种商品，统计了这种商品的销售价x（万元/吨）与月销售量y（吨）的关系 如表：
$\left\{\begin{array}{l}b=\frac{{\sum_{i=1}^n{（x_i-\overline x）（y_i-\overline y）}}}{{\sum_{i=1}^n{{{（x}_i-\overline x）}^2}}}\\ a=\overline y-b\overline x\end{array}\right.$
（1）已知y与x有关相关关系，并且可以用y=bx2+a来拟合，根据表中数据，建立y关于x 的回归方程；（b，a的结果保留整数位）
（2）已知这种商品的进价为2万元/吨，月利润为z万元，问销售价x（单位：万元/吨）为多少时，利润z最大？（精确到0.01，$\sqrt{3.04}=1.744$）
| X（万元） | 3 | 4 | 5 | 6 | 7 |
| Y（吨） | 90 | 83 | 75 | 65 | 52 |
（1）已知y与x有关相关关系，并且可以用y=bx2+a来拟合，根据表中数据，建立y关于x 的回归方程；（b，a的结果保留整数位）
（2）已知这种商品的进价为2万元/吨，月利润为z万元，问销售价x（单位：万元/吨）为多少时，利润z最大？（精确到0.01，$\sqrt{3.04}=1.744$）