题目内容
8.已知以直角坐标系的原点O为极点,以x的正半轴为极轴建立极坐标系,则极坐标方程为ρ=2cosθ对应的图形是(其中点M为圆心)( )| A. | 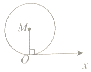 | B. | 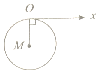 | C. | 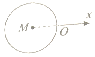 | D. | 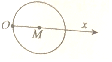 |
分析 求出圆的直角坐标方程为x2+y2-2x=0.圆心M(1,0),半径r=1.由此能求出结果.
解答 解:∵极坐标方程为ρ=2cosθ,
∴直角坐标方程为x2+y2-2x=0.
∴圆心M(1,0),半径r=$\frac{1}{2}\sqrt{(-2)^{2}}$=1.
故选:D.
点评 本题考查圆的位置的判断,考查直角坐标方程、极坐标方程、参数方程的互化等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,是中档题.

练习册系列答案
相关题目
19.22015被9除所得的余数是( )
| A. | 4 | B. | 5 | C. | 7 | D. | 8 |
16.对某校高二年级某班63名同学,在一次期末考试中的英语成绩作统计,得到如下的列联表:
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,参照附表,得到的正确结论是( )
| 不低于120分(优秀) | 低于120分(非优秀) | |
| 男 | 12 | 21 |
| 女 | 11 | 19 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
| A. | 在犯错误的概率不超过0.01的前提下认为“该班学生英语成绩优秀与性别有关” | |
| B. | 在犯错误的概率不超过0.05的前提下认为“该班学生英语成绩优秀与性别有关” | |
| C. | 没有90%以上的把握认为“该班学生英语成绩优秀与性别有关” | |
| D. | 有90%以上的把握认为“该班学生英语成绩优秀与性别有关” |
3. n个连续自然数按规律排成表:
n个连续自然数按规律排成表:
根据规律,从2016到2018,箭头的方向依次为( )
 n个连续自然数按规律排成表:
n个连续自然数按规律排成表:根据规律,从2016到2018,箭头的方向依次为( )
| A. | ↓→ | B. | →↑ | C. | ↑→ | D. | →↓ |
13.过点A(2,3)的直线的参数方程为$\left\{\begin{array}{l}{x=2+t}\\{y=3+2t}\end{array}\right.$(t为参数),若此直线与直线x-y+3=0相交于点B,则|AB|=( )
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 3$\sqrt{5}$ | D. | $\frac{3\sqrt{5}}{2}$ |
20. 如图,网格纸上小正方形的边长为1,粗线画出的一个三棱锥的三视图,则该三棱锥的表面积为( )
如图,网格纸上小正方形的边长为1,粗线画出的一个三棱锥的三视图,则该三棱锥的表面积为( )
 如图,网格纸上小正方形的边长为1,粗线画出的一个三棱锥的三视图,则该三棱锥的表面积为( )
如图,网格纸上小正方形的边长为1,粗线画出的一个三棱锥的三视图,则该三棱锥的表面积为( )| A. | $\frac{{15+\sqrt{17}}}{2}$ | B. | $\frac{{13+\sqrt{17}}}{2}$ | C. | $\frac{{11+\sqrt{17}}}{2}$ | D. | $\frac{{9+\sqrt{17}}}{2}$ |
17.两个分类变量X与Y有关系的可能性越大,随机变量K2的值( )
| A. | 越大 | B. | 越小 | ||
| C. | 不变 | D. | 可能越大也可能越小 |
18.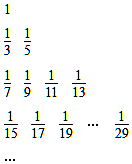 把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )
把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )
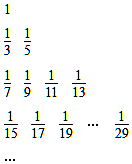 把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )
把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )| A. | $\frac{1}{99}$ | B. | $\frac{1}{87}$ | C. | $\frac{1}{81}$ | D. | $\frac{1}{85}$ |