题目内容
10.直线$ρcosθ=\frac{1}{2}$被圆ρ=1所截得的弦长为$\sqrt{3}$.分析 直线的普通方程为x=$\frac{1}{2}$,圆的普通方程为x2+y2=1,求出圆心(0,0)到直线x=$\frac{1}{2}$的距离d=$\frac{1}{2}$,由此能求出直线$ρcosθ=\frac{1}{2}$被圆ρ=1所截得的弦长.
解答 解:直线$ρcosθ=\frac{1}{2}$的普通方程为x=$\frac{1}{2}$,
圆ρ=1的x2+y2=1,
圆心(0,0)到直线x=$\frac{1}{2}$的距离d=$\frac{1}{2}$,
∴直线$ρcosθ=\frac{1}{2}$被圆ρ=1所截得的弦长:
|AB|=2$\sqrt{1-(\frac{1}{2})^{2}}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查直线被圆截得的弦长的求法,考查直角坐标方程、极坐标方程、参数方程的互化等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20. 如图,网格纸上小正方形的边长为1,粗线画出的一个三棱锥的三视图,则该三棱锥的表面积为( )
如图,网格纸上小正方形的边长为1,粗线画出的一个三棱锥的三视图,则该三棱锥的表面积为( )
 如图,网格纸上小正方形的边长为1,粗线画出的一个三棱锥的三视图,则该三棱锥的表面积为( )
如图,网格纸上小正方形的边长为1,粗线画出的一个三棱锥的三视图,则该三棱锥的表面积为( )| A. | $\frac{{15+\sqrt{17}}}{2}$ | B. | $\frac{{13+\sqrt{17}}}{2}$ | C. | $\frac{{11+\sqrt{17}}}{2}$ | D. | $\frac{{9+\sqrt{17}}}{2}$ |
1.已知△ABC的平面直观图△A′B′C′,是边长为a的正三角形,那么原△ABC的面积为( )
| A. | $\frac{\sqrt{3}}{2}$a 2 | B. | $\frac{\sqrt{3}}{4}$a 2 | C. | $\frac{\sqrt{6}}{2}$a 2 | D. | $\sqrt{6}$a 2 |
18.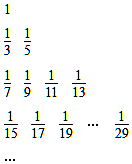 把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )
把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )
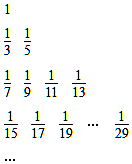 把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )
把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )| A. | $\frac{1}{99}$ | B. | $\frac{1}{87}$ | C. | $\frac{1}{81}$ | D. | $\frac{1}{85}$ |
15.在极坐标系中,点$(4,\frac{π}{3})$到直线$ρsin(θ-\frac{π}{3})=2$的距离是( )
| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | 1 |
2. 将正奇数1,3,5,7,…排成五列(如表),按此表的排列规律,2017所在的位置是( )
将正奇数1,3,5,7,…排成五列(如表),按此表的排列规律,2017所在的位置是( )
 将正奇数1,3,5,7,…排成五列(如表),按此表的排列规律,2017所在的位置是( )
将正奇数1,3,5,7,…排成五列(如表),按此表的排列规律,2017所在的位置是( )| A. | 第一列 | B. | 第二列 | C. | 第三列 | D. | 第四列 |
6.x2+y2=1经过伸缩变换$\left\{\begin{array}{l}{x′=2x}\\{y′=3y}\end{array}\right.$,后所得图形的焦距( )
| A. | 4 | B. | 2$\sqrt{13}$ | C. | 2$\sqrt{5}$ | D. | 6 |