题目内容
9.某公司出售某种商品,统计了这种商品的销售价x(万元/吨)与月销售量y(吨)的关系 如表:| X(万元) | 3 | 4 | 5 | 6 | 7 |
| Y(吨) | 90 | 83 | 75 | 65 | 52 |
(1)已知y与x有关相关关系,并且可以用y=bx2+a来拟合,根据表中数据,建立y关于x 的回归方程;(b,a的结果保留整数位)
(2)已知这种商品的进价为2万元/吨,月利润为z万元,问销售价x(单位:万元/吨)为多少时,利润z最大?(精确到0.01,$\sqrt{3.04}=1.744$)
分析 (1)求出y关于x2的线性回归方程即可,
(2)求出利润Z关于x的函数,根据二次函数的性质可得利润Z最大.
解答 解:(1)令m=x2,则y与m具有线性相关关系,m与y的对于关系如下:
| m | 9 | 16 | 25 | 36 | 49 |
| y | 90 | 83 | 75 | 65 | 52 |
设y关于m的回归方程为$\stackrel{∧}{y}$=$\stackrel{∧}{b}$m+$\stackrel{∧}{a}$,
则$\stackrel{∧}{b}$=-$\frac{954}{1014}$≈-1,$\stackrel{∧}{a}$=53-(-1)×27=80.
∴y关于m的回归方程为$\stackrel{∧}{y}$=-m+80,
∴y关于x的回归方程为$\stackrel{∧}{y}$=-x2+80.
(2)利润z关于销售价x的函数为z(x)=xy-2x=-x3+78x,x>0,
z′(x)=-3x2+78,令z′(x)=0得x=$\sqrt{26}$,
∴0<x<$\sqrt{26}$时,z′(x)>0,当x>$\sqrt{26}$时,z′(x)<0,
∴z(x)在(0,$\sqrt{26}$)上单调递增,在($\sqrt{26}$,+∞)上单调递减,
∴当x=$\sqrt{26}$≈5.10时,z(x)取得最大值z($\sqrt{26}$)≈265.15.
∴当定价为5.1万元时利润最大,最大利润为265.15万元.
点评 本题考查了二次拟合的回归方程求解,数值预测,属于中档题.

练习册系列答案
相关题目
19.22015被9除所得的余数是( )
| A. | 4 | B. | 5 | C. | 7 | D. | 8 |
20. 如图,网格纸上小正方形的边长为1,粗线画出的一个三棱锥的三视图,则该三棱锥的表面积为( )
如图,网格纸上小正方形的边长为1,粗线画出的一个三棱锥的三视图,则该三棱锥的表面积为( )
 如图,网格纸上小正方形的边长为1,粗线画出的一个三棱锥的三视图,则该三棱锥的表面积为( )
如图,网格纸上小正方形的边长为1,粗线画出的一个三棱锥的三视图,则该三棱锥的表面积为( )| A. | $\frac{{15+\sqrt{17}}}{2}$ | B. | $\frac{{13+\sqrt{17}}}{2}$ | C. | $\frac{{11+\sqrt{17}}}{2}$ | D. | $\frac{{9+\sqrt{17}}}{2}$ |
17.两个分类变量X与Y有关系的可能性越大,随机变量K2的值( )
| A. | 越大 | B. | 越小 | ||
| C. | 不变 | D. | 可能越大也可能越小 |
14.设ab<0,则下列四个式子:(1)|a-b|=|a|+|b|,(2)|a-b|<|a+b|,(3)|a+b|<|b|,(4)|a-b|>|a|-|b|中,正确的是( )
| A. | (1)、(2) | B. | (1)、(4) | C. | (3)、(4) | D. | (2)、(4) |
1.已知△ABC的平面直观图△A′B′C′,是边长为a的正三角形,那么原△ABC的面积为( )
| A. | $\frac{\sqrt{3}}{2}$a 2 | B. | $\frac{\sqrt{3}}{4}$a 2 | C. | $\frac{\sqrt{6}}{2}$a 2 | D. | $\sqrt{6}$a 2 |
18.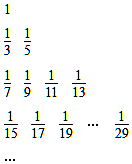 把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )
把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )
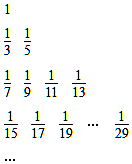 把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )
把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )| A. | $\frac{1}{99}$ | B. | $\frac{1}{87}$ | C. | $\frac{1}{81}$ | D. | $\frac{1}{85}$ |