题目内容
17.任取$θ∈(0,\frac{3}{2}π)$,则使sinθ>0的概率是$\frac{2}{3}$.分析 任取$θ∈(0,\frac{3}{2}π)$,使sinθ>0的θ∈(0,π),由此利用几何概型能求出使sinθ>0的概率.
解答 解:∵任取$θ∈(0,\frac{3}{2}π)$,
∴使sinθ>0的θ∈(0,π),
∴使sinθ>0的概率是p=$\frac{π}{\frac{3}{2}π}$=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题考查概率的求法,涉及到三角函数、几何概型等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.

练习册系列答案
相关题目
7.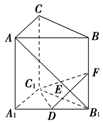 直三棱柱ABC-A1B1C1中,侧棱长为2,AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的动点,AB1,DF交于点E,要使AB1⊥平面C1DF,则线段B1F的长为( )
直三棱柱ABC-A1B1C1中,侧棱长为2,AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的动点,AB1,DF交于点E,要使AB1⊥平面C1DF,则线段B1F的长为( )
 直三棱柱ABC-A1B1C1中,侧棱长为2,AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的动点,AB1,DF交于点E,要使AB1⊥平面C1DF,则线段B1F的长为( )
直三棱柱ABC-A1B1C1中,侧棱长为2,AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的动点,AB1,DF交于点E,要使AB1⊥平面C1DF,则线段B1F的长为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
5.函数$f(x)=\frac{{\sqrt{x+2}}}{{{2^x}-1}}$的定义域为( )
| A. | [-2,+∞) | B. | (-2,+∞) | C. | (-2,0)∪(0,+∞) | D. | [-2,0)∪(0,+∞) |
12.若i是虚数单位,则复数$z=\frac{{1-\sqrt{3}i}}{2i}$在复平面内所对应的点位于( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
14.已知f(x)是定义在R上的函数,其导函数f'(x)满足f'(x)<f(x)(x∈R),则( )
| A. | f(2)>e2f(0),f(2001)>e2001f(0) | B. | f(2)<e2f(0),f(2001)>e2001f(0) | ||
| C. | f(2)>e2f(0),f(2001)<e2001f(0) | D. | f(2)<e2f(0),f(2001)<e2001f(0) |