题目内容
2.已知函数f(x)=$\frac{2-cos[\frac{π}{4}(1-x)]+sin[\frac{π}{4}(1-x)]}{{x}^{2}+4x+5}$(-4≤x≤0),则f(x)的最大值为2+$\sqrt{2}$.分析 运用两角和的余弦公式和诱导公式、二次函数的配方化简函数f(x),再由正弦函数的最值和二次函数的最值求法,即可得到所求最大值.
解答 解:f(x)=$\frac{2-cos[\frac{π}{4}(1-x)]+sin[\frac{π}{4}(1-x)]}{{x}^{2}+4x+5}$
=$\frac{2-\sqrt{2}cos(\frac{π}{4}-\frac{π}{4}x+\frac{π}{4})}{(x+2)^{2}+1}$
=$\frac{2-\sqrt{2}cos(\frac{π}{2}-\frac{π}{4}x)}{(x+2)^{2}+1}$=$\frac{2-\sqrt{2}sin(\frac{π}{4}x)}{(x+2)^{2}+1}$,
由-4≤x≤0,可得x=-2时,(x+2)2+1取得最小值1,
2-$\sqrt{2}$sin($\frac{π}{4}$x)在x=-2处取得最大值2+$\sqrt{2}$.
则f(x)的最大值为2+$\sqrt{2}$.
故答案为:2+$\sqrt{2}$.
点评 本题考查函数的最值的求法,注意运用两角和的余弦公式以及诱导公式、正弦函数的值域,以及二次函数的最值求法,考查运算能力,属于中档题.

练习册系列答案
相关题目
12.马路上亮着编号为1,2,3,4,5,6,7,8,9,10的10只路灯,为节约用电,现要求把其中的两只灯关掉,但不能同时关掉相邻的两只,也不能关掉两端的路灯,则满足条件的关灯方法共有几种( )
| A. | 12 | B. | 18 | C. | 21 | D. | 24 |
7.我国古代数学名著《数书九章》有“米谷粒分”题:粮仓开仓收粮,有人送来米1524石,验得米内夹谷,抽样取米一把,数得254粒内夹谷56粒,则这批米内夹谷约为( )
| A. | 1365石 | B. | 336石 | C. | 168石 | D. | 134石 |
19.一个几何体的三视图如图所示,则这个几何体的表面积为( )


| A. | 24+8$\sqrt{2}$+8$\sqrt{5}$ | B. | 20+8$\sqrt{2}$+4$\sqrt{5}$ | C. | 20+8$\sqrt{5}$+4$\sqrt{2}$ | D. | 20+4$\sqrt{2}$+4$\sqrt{5}$ |
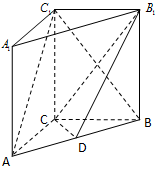 如图,在三棱柱ABC-A1B1C1中侧棱垂直于底面,AC⊥BC,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中侧棱垂直于底面,AC⊥BC,点D是AB的中点.