题目内容
6.在等差数列{an}中,已知a2=2,a4=4(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)设bn=2${\;}^{{a}_{n}}$,求数列{bn}前n项的和Sn.
分析 (1)通过a2=2、a4=4可求出数列{an}的公差为1,利用an=a2+(n-2)d计算可得结论;
(2)通过(1)可知bn=2n,进而利用等比数列的求和公式计算即得结论.
解答 解:(1)因为a2=2,a4=4,
所以$\frac{{a}_{4}-{a}_{2}}{4-2}$=1,即数列{an}的公差为1,
所以an=a2+(n-2)=n;
(2)由(1)可知bn=2n,
所以b1=2,q=2,
所以由等比数列的求和公式可知${S_n}=2({2^n}-1)$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于基础题.

练习册系列答案
相关题目
16.向量$\overrightarrow{AB}$,$\overrightarrow{CD}$,$\overrightarrow{EF}$在正方形网格中的位置如图所示,则( )


| A. | $\overrightarrow{EF}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{CD}$ | B. | $\overrightarrow{EF}$=$\frac{2}{3}$$\overrightarrow{AB}$$+\frac{1}{3}$$\overrightarrow{CD}$ | C. | $\overrightarrow{EF}$=$\overrightarrow{AB}$+$\overrightarrow{CD}$ | D. | $\overrightarrow{EF}$=$\frac{2}{3}$$\overrightarrow{AB}$$+\frac{2}{3}$$\overrightarrow{CD}$ |
2.与空间四边形ABCD四个顶点距离相等的平面共有( )
| A. | 7个 | B. | 6个 | C. | 5个 | D. | 4个 |
3.血药浓度(Plasma Concentration)是指药物吸收后在血浆内的总浓度.药物在人体内发挥治疗作用时,该药物的血药浓度应介于最低有效浓度和最低中毒浓度之间.已知成人单次服用1单位某药物后,体内血药浓度及相关信息如图所示:
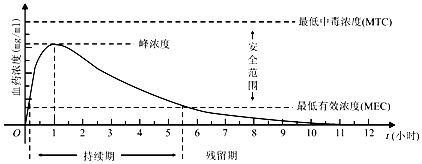
根据图中提供的信息,下列关于成人使用该药物的说法中,不正确的是( )

根据图中提供的信息,下列关于成人使用该药物的说法中,不正确的是( )
| A. | 首次服用该药物1单位约10分钟后,药物发挥治疗作用 | |
| B. | 每次服用该药物1单位,两次服药间隔小于2小时,一定会产生药物中毒 | |
| C. | 每间隔5.5小时服用该药物1单位,可使药物持续发挥治疗作用 | |
| D. | 首次服用该药物1单位3小时后,再次服用该药物1单位,不会发生药物中毒 |
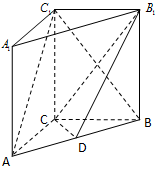 如图,在三棱柱ABC-A1B1C1中侧棱垂直于底面,AC⊥BC,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中侧棱垂直于底面,AC⊥BC,点D是AB的中点.