题目内容
5.函数$f(x)=\frac{{\sqrt{x+2}}}{{{2^x}-1}}$的定义域为( )| A. | [-2,+∞) | B. | (-2,+∞) | C. | (-2,0)∪(0,+∞) | D. | [-2,0)∪(0,+∞) |
分析 根据函数的解析式,列出使解析式有意义的不等式组,求出解集即可.
解答 解:函数$f(x)=\frac{{\sqrt{x+2}}}{{{2^x}-1}}$,
∴$\left\{\begin{array}{l}{x+2≥0}\\{{2}^{x}-1≠0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x≥-2}\\{x≠0}\end{array}\right.$,
即x≥-2或x≠0;
∴f(x)的定义域为[-2,0)∪(0,+∞).
故选:D.
点评 本题考查了根据函数解析式求定义域的应用问题,是基础题.

练习册系列答案
相关题目
16.向量$\overrightarrow{AB}$,$\overrightarrow{CD}$,$\overrightarrow{EF}$在正方形网格中的位置如图所示,则( )


| A. | $\overrightarrow{EF}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{CD}$ | B. | $\overrightarrow{EF}$=$\frac{2}{3}$$\overrightarrow{AB}$$+\frac{1}{3}$$\overrightarrow{CD}$ | C. | $\overrightarrow{EF}$=$\overrightarrow{AB}$+$\overrightarrow{CD}$ | D. | $\overrightarrow{EF}$=$\frac{2}{3}$$\overrightarrow{AB}$$+\frac{2}{3}$$\overrightarrow{CD}$ |
2.与空间四边形ABCD四个顶点距离相等的平面共有( )
| A. | 7个 | B. | 6个 | C. | 5个 | D. | 4个 |
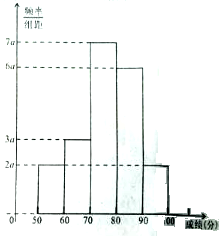 20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.
20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.