题目内容
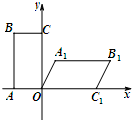如图，矩形OABC和平行四边形OA1B1C1的部分顶点坐标为：A（-1，0），B（-1，2），A1（| 1 |
| 2 |
（Ⅰ）求将矩形OABC变为平行四边形OA1B1C1的线性变换对应的矩阵M；
（Ⅱ）矩阵M是否存在特征值？若存在，求出矩阵M的所有特征值及其对应的一个特征向量；若不存在，请说明理由．
考点：特征值与特征向量的计算,几种特殊的矩阵变换
专题：计算题,矩阵和变换
分析：（Ⅰ）设M=
，依题意得C（0，2），依题意得=
•
=
，由矩阵乘法解出a，b，c，d即可；
（II）由矩阵的特征多项式f（λ）=
，令它为0，即可得到特征值和特征向量．
|
|
|
|
（II）由矩阵的特征多项式f（λ）=
|
解答：
解：（Ⅰ）设M=
，依题意得C（0，2）
依题意得=
•
=
，
即
，所以
所以M=
；
（II）因为矩阵M的特征方程f（λ）=
=λ2+
λ+1=0无解，
所以矩阵M没有特征值也没有特征向量．
|
依题意得=
|
|
|
即
|
|
所以M=
|
（II）因为矩阵M的特征方程f（λ）=
|
| 1 |
| 2 |
所以矩阵M没有特征值也没有特征向量．
点评：本题考查矩阵变换与矩阵的求法，考查矩阵特征值与特征向量的计算等基础知识，属于基础题．
练习册系列答案
相关题目
