题目内容
已知函数y=（ex-a）2+（e-x-a）2，（a＞2），则函数y的最小值为 ．
考点：函数的最值及其几何意义
专题：函数的性质及应用
分析：将函数进行化简，利用换元法结合一元二次函数的性质即可得到结论．
解答：
解：y=（ex-a）2+（e-x-a）2=（ex+e-x）2-2a（ex+e-x）+2a2-2，
设t=ex+e-x，则t=ex+e-x≥2
=2，
则y=t2-2at+2a2-2=（t-a）2+a2-2，
∵a＞2，t≥2，
∴当t=a时，y=（t-a）2+a2-2取得最小值a2-2，
故答案为：a2-2．
设t=ex+e-x，则t=ex+e-x≥2
| ex•e-x |
则y=t2-2at+2a2-2=（t-a）2+a2-2，
∵a＞2，t≥2，
∴当t=a时，y=（t-a）2+a2-2取得最小值a2-2，
故答案为：a2-2．
点评：本题主要考查函数最值的求解，根据指数幂的化简公式以及利用换元法转化为一元二次函数，利用一元二次函数的性质是解决本题的关键．
练习册系列答案
相关题目
如图，四边形ABCD中，AB=2，C=2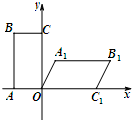
如图，矩形OABC和平行四边形OA1B1C1的部分顶点坐标为：A（-1，0），B（-1，2），A1（