题目内容
已知函数f(x)=
sinωx•cosωx+cos2ωx+1(ω>0)的最小正周期为π.
(1)求ω的值;
(2)求当x∈(0,
]时f(x)的值域.
| 3 |
(1)求ω的值;
(2)求当x∈(0,
| π |
| 2 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的求值
分析:(1)由条件利用三角恒等变换化简函数的解析式为f(x)=sin(2ωx+
)+
,由此根据周期为π求得ω的值.
(2)当x∈(0,
]时,利用正弦函数的定义域和值域求得f(x)的值域.
| π |
| 6 |
| 3 |
| 2 |
(2)当x∈(0,
| π |
| 2 |
解答:
解:(1)f(x)=
sinωxcosωx+
+1=
sin2ωx+
cos2ωx+
=sin(2ωx+
)+
.
∵ω>0,∴T=
=π,∴ω=2.
(2)由(1)得:f(x)=sin(2ωx+
)+
,∵0<x≤
,∴
<2x+
≤
,
∴-
≤sin(2x+
)≤1,∴1≤f(x)≤
,即f(x)的值域是[1,
].
| 3 |
| 1+cos2ωx |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| π |
| 6 |
| 3 |
| 2 |
∵ω>0,∴T=
| 2π |
| ω |
(2)由(1)得:f(x)=sin(2ωx+
| π |
| 6 |
| 3 |
| 2 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∴-
| 1 |
| 2 |
| π |
| 6 |
| 5 |
| 2 |
| 5 |
| 2 |
点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的周期性、定义域和值域,属于基础题.

练习册系列答案
相关题目
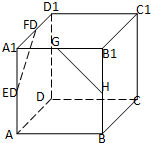 如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别是AA1,A1D1,A1B1,BB1的中点,则异面直线EF与GH所成的角的大小为( )
如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别是AA1,A1D1,A1B1,BB1的中点,则异面直线EF与GH所成的角的大小为( )| A、30° | B、45° |
| C、60° | D、120° |
 如图,四边形ABCD中,AB=2,C=2
如图,四边形ABCD中,AB=2,C=2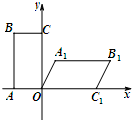 如图,矩形OABC和平行四边形OA1B1C1的部分顶点坐标为:A(-1,0),B(-1,2),A1(
如图,矩形OABC和平行四边形OA1B1C1的部分顶点坐标为:A(-1,0),B(-1,2),A1(