题目内容
已知f(x)是一次函数,且满足3f(x+1)-2f(x-1)=2x+17;
(1)求f(x);
(2)求当x∈(-1,3]时,f(x)的值域.
(1)求f(x);
(2)求当x∈(-1,3]时,f(x)的值域.
考点:抽象函数及其应用,函数的值域
专题:计算题,函数的性质及应用
分析:(1)由题意设f(x)=ax+b,利用f(x)满足3f(x+1)-2f(x-1)=2x+17,利用恒等式的性质即可得出;
(2)由f(x)的单调性,即可得到值域.
(2)由f(x)的单调性,即可得到值域.
解答:
解:(1)由题意设f(x)=ax+b,(a≠0).
∵f(x)满足3f(x+1)-2f(x-1)=2x+17,
∴3[a(x+1)+b]-2[a(x-1)+b]=2x+17,
化为ax+(5a+b)=2x+17,
∴
,解得
.
∴f(x)=2x+7.
(2)∵f(x)在R上单调递增,
∴当x∈(-1,3]时,f(x)∈(-2+7,2×3+7],
∴f(x)的值域为(5,13].
∵f(x)满足3f(x+1)-2f(x-1)=2x+17,
∴3[a(x+1)+b]-2[a(x-1)+b]=2x+17,
化为ax+(5a+b)=2x+17,
∴
|
|
∴f(x)=2x+7.
(2)∵f(x)在R上单调递增,
∴当x∈(-1,3]时,f(x)∈(-2+7,2×3+7],
∴f(x)的值域为(5,13].
点评:本题考查了“待定系数法”求一次函数的解析式和恒等式的性质,同时考查一次函数的单调性及运用:求值域,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
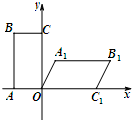 如图,矩形OABC和平行四边形OA1B1C1的部分顶点坐标为:A(-1,0),B(-1,2),A1(
如图,矩形OABC和平行四边形OA1B1C1的部分顶点坐标为:A(-1,0),B(-1,2),A1(