题目内容
已知二次函数f(x)=ax2+bx满足f(2)=0,且方程f(x)=x有等根.
(1)求f(x)的解析式;
(2)求f(x)的值域;
(3)是否存在实数m、n(m<n),使f(x)的定义域和值域分别为[m,n]和[4m,4n].若存在,求出m、n的值;若不存在,请说明理由.
(1)求f(x)的解析式;
(2)求f(x)的值域;
(3)是否存在实数m、n(m<n),使f(x)的定义域和值域分别为[m,n]和[4m,4n].若存在,求出m、n的值;若不存在,请说明理由.
考点:函数的值域,函数的定义域及其求法,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)根据f(2)=0得4a+2b=0,根据f(x)=x有等根可求出b=1,这样即可解出a,从而求出f(x)=-
x2+x;
(2)对f(x)进行配方即可求出f(x)的值域;
(3)根据题意知,对于函数y=4x,它的定义域若是[m,n],值域便是[4m,4n],所以求函数y=4x图象和函数f(x)的图象的交点,若有两个交点,便符合已知条件,若没有交点或只一个交点,便不存在已知条件中的m,n,所以解方程组
即得答案.
| 1 |
| 2 |
(2)对f(x)进行配方即可求出f(x)的值域;
(3)根据题意知,对于函数y=4x,它的定义域若是[m,n],值域便是[4m,4n],所以求函数y=4x图象和函数f(x)的图象的交点,若有两个交点,便符合已知条件,若没有交点或只一个交点,便不存在已知条件中的m,n,所以解方程组
|
解答:
解:(1)由f(2)=0得:4a+2b=0 ①;
由f(x)=x得:ax2+bx=x,∴x(ax+b-1)=0,∵该方程有等根,∴等根为0,∴0+b-1=0,∴b=1,将b=1带入①得:a=-
;
∴f(x)=-
x2+x;
(2)f(x)=-
x2+x=-
(x-1)2+
≤
,∴f(x)的值域为(-∞,
];
(3)令y=f(x),解
得x=0,y=0或x=-6,y=-24;
∴存在m=-6,n=0,使f(x)的定义域和值域分别为[m,n],[4m,4n].
由f(x)=x得:ax2+bx=x,∴x(ax+b-1)=0,∵该方程有等根,∴等根为0,∴0+b-1=0,∴b=1,将b=1带入①得:a=-
| 1 |
| 2 |
∴f(x)=-
| 1 |
| 2 |
(2)f(x)=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)令y=f(x),解
|
∴存在m=-6,n=0,使f(x)的定义域和值域分别为[m,n],[4m,4n].
点评:考查求函数解析式,及等根的概念,用配方法求二次函数的值域,判断求f(x)的定义域,值域分别为[m,n],[4m,4n],即判断f(x)和y=4x图象有两个以上交点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
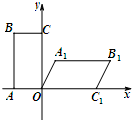 如图,矩形OABC和平行四边形OA1B1C1的部分顶点坐标为:A(-1,0),B(-1,2),A1(
如图,矩形OABC和平行四边形OA1B1C1的部分顶点坐标为:A(-1,0),B(-1,2),A1(