题目内容
如图1,∠ACB=45°,BC=3,过动点A作AD⊥BC,垂足D在线段BC上且异于点B,连接AB,沿AD将△ABD折起,使∠BDC=90°(如图2所示).M为棱AC的中点.
(1)求证:AD⊥BC;
(2)当三棱锥A-BCD的体积最大时,求直线BM与面ACD所成角的正弦值.
(1)求证:AD⊥BC;
(2)当三棱锥A-BCD的体积最大时,求直线BM与面ACD所成角的正弦值.
考点:直线与平面所成的角
专题:空间位置关系与距离,空间角
分析:(1)沿AD将△ABD折起后,AD⊥BD,AD⊥DC,从而AD⊥平面BDC,由此能证明AD⊥BC.
(2)以D为原点,建立空间直角坐标系D-xyz,利用向量法能证明直线BM与面ACD所成角的正弦值.
(2)以D为原点,建立空间直角坐标系D-xyz,利用向量法能证明直线BM与面ACD所成角的正弦值.
解答:
(1)证明:∵AD⊥BC,
∴沿AD将△ABD折起后,AD⊥BD,AD⊥DC,
又BD∩DC=D,∴AD⊥平面BDC,
又BC?平面BDC,∴AD⊥BC.
(2)∵∠BDC=90°,∴DB,DC,DA两两垂直,
以D为原点,建立空间直角坐标系D-xyz,
设BD=x,则CD=3-x∵∠ACB=45°,AD⊥BC,∴AD=CD=3-x,
∵折起前AD⊥BC,∴折起后AD⊥BD,AD⊥CD,BD∩DC=D
∴AD⊥平面BCD,
∴VA-BCD=
×AD×S△BCD=
×(3-x)×
×x(3-x)=
(x3-6x2+9x)
设f(x)=
(x3-6x2+9x),x∈(0,3),
∵f′(x)=
(x-1)(x-3),
∴f(x)在(0,1)上为增函数,在(1,3)上为减函数,
∴当x=1时,函数f(x)取最大值
∴当BD=1时,三棱锥A-BCD的体积最大.
三棱锥A-BCD的体积最大时,BD=1,AD=CD=2
∴D(0,0,0),B(1,0,0),C(0,2,0),
A(0,0,2),M(0,1,1),E(
,1,0),
且
=(-1,1,1),
设直线BM与面ACD所成角为θ,
∵平面ACD的法向量
=(1,0,0)
∴sinθ=|cos<
,
>|=|
|=
.
∴直线BM与面ACD所成角的正弦值为
.
∴沿AD将△ABD折起后,AD⊥BD,AD⊥DC,

又BD∩DC=D,∴AD⊥平面BDC,
又BC?平面BDC,∴AD⊥BC.
(2)∵∠BDC=90°,∴DB,DC,DA两两垂直,
以D为原点,建立空间直角坐标系D-xyz,
设BD=x,则CD=3-x∵∠ACB=45°,AD⊥BC,∴AD=CD=3-x,
∵折起前AD⊥BC,∴折起后AD⊥BD,AD⊥CD,BD∩DC=D
∴AD⊥平面BCD,
∴VA-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
设f(x)=
| 1 |
| 6 |
∵f′(x)=
| 1 |
| 2 |
∴f(x)在(0,1)上为增函数,在(1,3)上为减函数,
∴当x=1时,函数f(x)取最大值
∴当BD=1时,三棱锥A-BCD的体积最大.
三棱锥A-BCD的体积最大时,BD=1,AD=CD=2
∴D(0,0,0),B(1,0,0),C(0,2,0),
A(0,0,2),M(0,1,1),E(
| 1 |
| 2 |
且
| BM |
设直线BM与面ACD所成角为θ,
∵平面ACD的法向量
| m |
∴sinθ=|cos<
| m |
| BM |
| -1 | ||
|
| ||
| 3 |
∴直线BM与面ACD所成角的正弦值为
| ||
| 3 |
点评:本题考查异面直线垂直的证明,考查直线与平面所成角的正弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
 如图,四边形ABCD中,AB=2,C=2
如图,四边形ABCD中,AB=2,C=2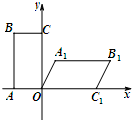 如图,矩形OABC和平行四边形OA1B1C1的部分顶点坐标为:A(-1,0),B(-1,2),A1(
如图,矩形OABC和平行四边形OA1B1C1的部分顶点坐标为:A(-1,0),B(-1,2),A1(