题目内容
10.《最强大脑》是大型科学竞技类真人秀节目,是专注传播脑科学知识和脑力竞技的节目.某机构为了了解大学生喜欢《最强大脑》是否与性别有关,对某校的100名大学生进行了问卷调查,得到如下列联表:| 喜欢《最强大脑》 | 不喜欢《最强大脑》 | 合计 | |
| 男生 | 15 | ||
| 女生 | 15 | ||
| 合计 |
( I)请将上述列联表补充完整;判断是否有99.9%的把握认为喜欢《最强大脑》与性别有关,并说明理由;
( II)已知在被调查的大学生中有5名是大一学生,其中3名喜欢《最强大脑》,现从这5名大一学生中随机抽取2人,抽到喜欢《最强大脑》的人数为X,求X的分布列及数学期望.
下面的临界值表仅参考:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (Ⅰ)由题意知完成列联表,求出K2≈14.063>10.828,由此有99.9%的把握认为喜欢《最强大脑》与性别有关.
(II)X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和EX.
解答 解:(Ⅰ)由题意知列联表为:
| 喜欢《最强大脑》 | 不喜欢《最强大脑》 | 合计 | |
| 男生 | 45 | 15 | 60 |
| 女生 | 15 | 25 | 40 |
| 合计 | 60 | 40 | 100 |
∴有99.9%的把握认为喜欢《最强大脑》与性别有关.
(II)X的可能取值为0,1,2,
P(X=0)=$\frac{{C}_{2}^{2}}{{C}_{5}^{2}}$=$\frac{1}{10}$,
P(X=1)=$\frac{{C}_{2}^{1}{C}_{3}^{1}}{{C}_{5}^{2}}$=$\frac{3}{5}$,
P(X=2)=$\frac{{C}_{3}^{2}}{{C}_{5}^{2}}$=$\frac{3}{10}$,
∴X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{1}{10}$ | $\frac{3}{5}$ | $\frac{3}{10}$ |
点评 本题考查独立检验、离散型随机变量的分布列、数学期望等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、是中档题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
20.设z是复数,|z-i|≤2(i是虚数单位),则|z|的最大值是 ( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
15.已知x∈R,符号[x]表示不超过x的最大整数,f(x)=$\left\{\begin{array}{l}{[x],x≤0}\\{\frac{1}{x},x>0}\end{array}\right.$,则使方程$\frac{f(x)}{x}$=m恰有三个实根的实数m的取值范围是( )
| A. | ($\frac{1}{2}$,$\frac{2}{3}$) | B. | (1,$\frac{3}{2}$) | C. | ($\frac{4}{3}$,$\frac{3}{2}$] | D. | [$\frac{3}{2}$,2) |
19.集合A={x|y=lg(x-2)},B={y|y=2x,x≥0},则(∁RA)∩B=( )
| A. | (0,2) | B. | [0,2] | C. | [1,2] | D. | (1,2) |
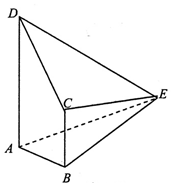 如图,在四棱锥E-ABCD中,平面CDE⊥平面ABCD,∠DAB=∠ABC=90°,AB=BC=1,AD=ED=3,EC=2.
如图,在四棱锥E-ABCD中,平面CDE⊥平面ABCD,∠DAB=∠ABC=90°,AB=BC=1,AD=ED=3,EC=2.