题目内容
19．集合A={x|y=lg（x-2）}，B={y|y=2x，x≥0}，则（∁RA）∩B=（ ）| A． | （0，2） | B． | [0，2] | C． | [1，2] | D． | （1，2） |
分析 求函数定义域得集合A，求值域得集合B，根据补集与交集的定义写出（∁RA）∩B．
解答 解：集合A={x|y=lg（x-2）}={x|x-2＞0}={x|x＞2}，
B={y|y=2x，x≥0}={y|y≥1}=[1，+∞）；
∴∁RA=（-∞，2]，
∴（∁RA）∩B=[1，2]．
故选：C．
点评 本题考查了求函数的定义域、值域的应用问题，也考查了集合的运算问题，是基础题．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
9．若方程|lnx|=a有两个不等的实根x1和x2，则x1+x2的取值范围是（ ）
| A． | （1，+∞） | B． | （$\sqrt{2}$，+∞） | C． | （2，+∞） | D． | （0，1） |
10．《最强大脑》是大型科学竞技类真人秀节目，是专注传播脑科学知识和脑力竞技的节目．某机构为了了解大学生喜欢《最强大脑》是否与性别有关，对某校的100名大学生进行了问卷调查，得到如下列联表：
已知在这100人中随机抽取1人抽到不喜欢《最强大脑》的大学生的概率为0.4
（ I）请将上述列联表补充完整；判断是否有99.9%的把握认为喜欢《最强大脑》与性别有关，并说明理由；
（ II）已知在被调查的大学生中有5名是大一学生，其中3名喜欢《最强大脑》，现从这5名大一学生中随机抽取2人，抽到喜欢《最强大脑》的人数为X，求X的分布列及数学期望．
下面的临界值表仅参考：
（参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
| 喜欢《最强大脑》 | 不喜欢《最强大脑》 | 合计 | |
| 男生 | 15 | ||
| 女生 | 15 | ||
| 合计 |
（ I）请将上述列联表补充完整；判断是否有99.9%的把握认为喜欢《最强大脑》与性别有关，并说明理由；
（ II）已知在被调查的大学生中有5名是大一学生，其中3名喜欢《最强大脑》，现从这5名大一学生中随机抽取2人，抽到喜欢《最强大脑》的人数为X，求X的分布列及数学期望．
下面的临界值表仅参考：
| P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
4．已知定义在R上的函数f（x）周期为2，且满足$f（x）=\left\{\begin{array}{l}x+a，-1≤x＜0\\|{\frac{2}{5}-x}|，0≤x＜1\end{array}\right.$，若$f（-\frac{5}{2}）=f（\frac{9}{2}）$，则f（5a）=（ ）
| A． | $\frac{7}{16}$ | B． | $-\frac{2}{5}$ | C． | $\frac{11}{16}$ | D． | $\frac{13}{16}$ |
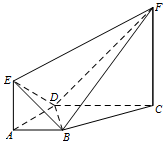已知几何体ABCDEF中，AB∥CD，AD⊥DC，EA⊥平面ABCD，FC∥EA，AB=AD=EA=1，CD=CF=2．