题目内容
2.已知f(x)=(1-a)lnx+$\frac{a}{2}$x2-x(a>0).(Ⅰ)当a=3时,其曲线在(1,f(1))处的切线方程;
(Ⅱ)讨论f(x)的单调性;
(Ⅲ)若f(x)在(1,2)有零点,求a的取值范围.
分析 (1)根据导数的几何意义即可求出切线方程,
(Ⅱ)先求导,再分类讨论,根据导数和函数的单调性的关系即可求出,
(Ⅲ)结合(Ⅱ)的结论,根据函数零点存在定理,即可求出a的范围.
解答 解:(Ⅰ)当a=3时,f(x)=-2lnx+$\frac{3}{2}$x2-x,
∴f′(x)=-$\frac{2}{x}$+3x-1,
∴k=f′(1)=-2+3-1=0,f(1)=$\frac{1}{2}$,
∴曲线在(1,f(1))处的切线方程为y=$\frac{1}{2}$;
(Ⅱ)∵f′(x)=$\frac{1-a}{x}$+ax-1=$\frac{a{x}^{2}-x+(1-a)}{x}$=$\frac{(x-1)(ax-a+1)}{x}$=$\frac{(x-1)(x-\frac{a-1}{a})}{ax}$,
令f′(x)=0,解得x=1,或x=1-$\frac{1}{a}$,且1>1-$\frac{1}{a}$
①当0<a<1时,1-$\frac{1}{a}$<0,
当f′(x)>0时,解得0<x<1,函数f(x)单调递增,
当f′(x)<0时,解得x>1,函数f(x)单调递减,
②当a>1时,1-$\frac{1}{a}$>0,
当f′(x)>0时,解得0<x<1-$\frac{1}{a}$或x>1时,函数f(x)单调递增,
当f′(x)<0时,解得1-$\frac{1}{a}$<x<1,函数f(x)单调递减,
③当a=1时,1-$\frac{1}{a}$=0,
当f′(x)>0时,解得x>1,函数f(x)单调递增,
当f′(x)<0时,解得0<x<1,函数f(x)单调递减,
综上所述,当0<a<1时,函数f(x)在(0,1)上递增,在(1,+∞)上递减,
当a=1时,函数f(x)在(0,1)上递减,在(1,+∞)上递增,
当a>1时,函数f(x)在(0,1-$\frac{1}{a}$),(1,+∞)递增,在(1-$\frac{1}{a}$,1)上递减
(Ⅲ)由(Ⅱ)可知,①当0<a<1时,函数f(x)在(1,2)上递减,
∴f(x)<f(1)=1-$\frac{a}{2}$<0,
∴f(x)在(1,2)上为无零点
②当a=1时,函数f(x)在(1,2)上递增,
f(1)=-$\frac{1}{2}$<0,f(2)=0,
∴f(x)在(1,2)上为无零点
当a>1时,函数f(x)在(1,2)递增,
∵f(x)在(1,2)有零点,
∴f(1)•f(2)<0,
∴($\frac{a}{2}$-1)(a-1)(2-ln2)<0,
即(a-2)(a-1)<0,
解得1<a<2,
综上所述a的取值范围为(1,2).
点评 本题考查了导数的几何意义以及导数和函数的单调性关系以及函数零点的问题,关键是分类讨论,考查了学生的分析解决问题的能力和转化能力,属于难题.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案| 喜欢《最强大脑》 | 不喜欢《最强大脑》 | 合计 | |
| 男生 | 15 | ||
| 女生 | 15 | ||
| 合计 |
( I)请将上述列联表补充完整;判断是否有99.9%的把握认为喜欢《最强大脑》与性别有关,并说明理由;
( II)已知在被调查的大学生中有5名是大一学生,其中3名喜欢《最强大脑》,现从这5名大一学生中随机抽取2人,抽到喜欢《最强大脑》的人数为X,求X的分布列及数学期望.
下面的临界值表仅参考:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | f(1)<2016f($\root{3}{2016}$)<2017f($\root{3}{2017}$) | B. | 2017f($\root{3}{2017}$)<f(1)<2016f($\root{3}{2016}$) | ||
| C. | 2016f($\root{3}{2016}$)<f(1)<2017f($\root{3}{2017}$) | D. | 2017f($\root{3}{2017}$)<2016f($\root{3}{2016}$)<f(1) |
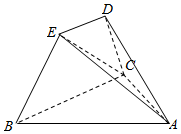 如图所示,四棱锥A-BCDE,已知平面BCDE⊥平面ABC,BE⊥EC,DE∥BC,BC=2DE=6,AB=4$\sqrt{3}$,∠ABC=30°.
如图所示,四棱锥A-BCDE,已知平面BCDE⊥平面ABC,BE⊥EC,DE∥BC,BC=2DE=6,AB=4$\sqrt{3}$,∠ABC=30°.