题目内容
1.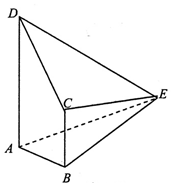 如图,在四棱锥E-ABCD中,平面CDE⊥平面ABCD,∠DAB=∠ABC=90°,AB=BC=1,AD=ED=3,EC=2.
如图,在四棱锥E-ABCD中,平面CDE⊥平面ABCD,∠DAB=∠ABC=90°,AB=BC=1,AD=ED=3,EC=2.(1)证明:AB⊥平面BCE;
(2)求直线AE与平面CDE所成角的正弦值.
分析 (1)推导出EC⊥CD,从而CE⊥面ABCD,再由CE⊥AB,AB⊥BC,由此能证明AB⊥面BCE.
(2)过A作AH⊥DC,交DC于H,则AH⊥平面DCE,连结EH,则∠AEH是直线AE与平面DCE所成的平面角,由此能证明直线AE与平面CDE所成角的正弦值.
解答 证明:(1)∵∠DAB=∠ABC=90°,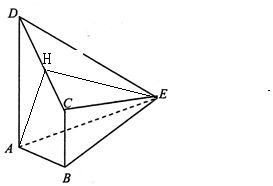
∴四边形ABCD是直角梯形,
∵AB=BC=1,AD=ED=3,EC=2.
∴CD=$\sqrt{{1}^{2}+(3-1)^{2}}$=$\sqrt{5}$,
∴CE2+DC2=DE2,∴EC⊥CD,
∵面EDC⊥面ABCD,面EDC∩面ABCD=DC,
∴CE⊥面ABCD,
∴CE⊥AB,又AB⊥BC,BC∩CE=C,
∴AB⊥面BCE.
解:(2)过A作AH⊥DC,交DC于H,
则AH⊥平面DCE,连结EH,
则∠AEH是直线AE与平面DCE所成的平面角,
∵$\frac{1}{2}×DC×AH$=$\frac{AD+BC}{2}×AB-\frac{1}{2}×AB×BC$,
∴AH=$\frac{\frac{1}{2}(3+1)×1-\frac{1}{2}×1×1}{\frac{1}{2}×\sqrt{5}}$=$\frac{3\sqrt{5}}{5}$,
AE=$\sqrt{A{B}^{2}+(C{E}^{2}+B{C}^{2})}$=$\sqrt{6}$,
∴sin∠AEH=$\frac{\sqrt{30}}{10}$,
∴直线AE与平面CDE所成角的正弦值为$\frac{\sqrt{30}}{10}$.
点评 本题考查线面垂直的证明,考查线面所成角的正弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想,是中档题.

| A. | (1,+∞) | B. | ($\sqrt{2}$,+∞) | C. | (2,+∞) | D. | (0,1) |
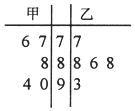
| A. | 甲乙得分的中位数相同 | B. | 乙的成绩较甲更稳定 | ||
| C. | 甲的平均分比乙高 | D. | 乙的平均分低于其中位数 |
| 喜欢《最强大脑》 | 不喜欢《最强大脑》 | 合计 | |
| 男生 | 15 | ||
| 女生 | 15 | ||
| 合计 |
( I)请将上述列联表补充完整;判断是否有99.9%的把握认为喜欢《最强大脑》与性别有关,并说明理由;
( II)已知在被调查的大学生中有5名是大一学生,其中3名喜欢《最强大脑》,现从这5名大一学生中随机抽取2人,抽到喜欢《最强大脑》的人数为X,求X的分布列及数学期望.
下面的临界值表仅参考:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |