题目内容
15.已知x∈R,符号[x]表示不超过x的最大整数,f(x)=$\left\{\begin{array}{l}{[x],x≤0}\\{\frac{1}{x},x>0}\end{array}\right.$,则使方程$\frac{f(x)}{x}$=m恰有三个实根的实数m的取值范围是( )| A. | ($\frac{1}{2}$,$\frac{2}{3}$) | B. | (1,$\frac{3}{2}$) | C. | ($\frac{4}{3}$,$\frac{3}{2}$] | D. | [$\frac{3}{2}$,2) |
分析 作出f(x)与y=mx的函数图象,根据图象有3个交点判断m的范围.
解答  解:由$\frac{f(x)}{x}=m$得f(x)=mx(x≠0),
解:由$\frac{f(x)}{x}=m$得f(x)=mx(x≠0),
作出f(x)与y=mx的函数图象,
∵方程$\frac{f(x)}{x}$=m恰有三个实根,
∴y=mx与y=f(x)(x≠0)的函数图象有3个交点,
当直线y=mx过点(-1,-2)时,m=2,
当直线y=mx经过点(-2,-3时),m=$\frac{3}{2}$,
∴$\frac{3}{2}$≤m<2.
故选D.
点评 本题考查了方程的根与函数图象的关系,属于中档题.

练习册系列答案
相关题目
6.如图茎叶图表示一次朗诵比赛中甲乙两位选手的得分,则下列说法错误的是( )
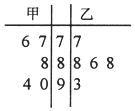

| A. | 甲乙得分的中位数相同 | B. | 乙的成绩较甲更稳定 | ||
| C. | 甲的平均分比乙高 | D. | 乙的平均分低于其中位数 |
3.已知双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1(a>0,b>0)$的离心率为$\sqrt{3}$,则该双曲线的渐近线方程为( )
| A. | $x-\sqrt{2}y=0$ | B. | $\sqrt{2}x-y=0$ | C. | $\sqrt{2}x±y=0$ | D. | $x±\sqrt{2}y=0$ |
10.《最强大脑》是大型科学竞技类真人秀节目,是专注传播脑科学知识和脑力竞技的节目.某机构为了了解大学生喜欢《最强大脑》是否与性别有关,对某校的100名大学生进行了问卷调查,得到如下列联表:
已知在这100人中随机抽取1人抽到不喜欢《最强大脑》的大学生的概率为0.4
( I)请将上述列联表补充完整;判断是否有99.9%的把握认为喜欢《最强大脑》与性别有关,并说明理由;
( II)已知在被调查的大学生中有5名是大一学生,其中3名喜欢《最强大脑》,现从这5名大一学生中随机抽取2人,抽到喜欢《最强大脑》的人数为X,求X的分布列及数学期望.
下面的临界值表仅参考:
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 喜欢《最强大脑》 | 不喜欢《最强大脑》 | 合计 | |
| 男生 | 15 | ||
| 女生 | 15 | ||
| 合计 |
( I)请将上述列联表补充完整;判断是否有99.9%的把握认为喜欢《最强大脑》与性别有关,并说明理由;
( II)已知在被调查的大学生中有5名是大一学生,其中3名喜欢《最强大脑》,现从这5名大一学生中随机抽取2人,抽到喜欢《最强大脑》的人数为X,求X的分布列及数学期望.
下面的临界值表仅参考:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
4.已知定义在R上的函数f(x)周期为2,且满足$f(x)=\left\{\begin{array}{l}x+a,-1≤x<0\\|{\frac{2}{5}-x}|,0≤x<1\end{array}\right.$,若$f(-\frac{5}{2})=f(\frac{9}{2})$,则f(5a)=( )
| A. | $\frac{7}{16}$ | B. | $-\frac{2}{5}$ | C. | $\frac{11}{16}$ | D. | $\frac{13}{16}$ |
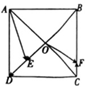 如图,边长为4的正方形ABCD中,AC与BD交于点O,$\overrightarrow{BE}$=$\frac{3}{4}$$\overrightarrow{BD}$,$\overrightarrow{CF}$=$\frac{1}{4}$$\overrightarrow{CB}$,则$\overrightarrow{AE}$•$\overrightarrow{OF}$等于( )
如图,边长为4的正方形ABCD中,AC与BD交于点O,$\overrightarrow{BE}$=$\frac{3}{4}$$\overrightarrow{BD}$,$\overrightarrow{CF}$=$\frac{1}{4}$$\overrightarrow{CB}$,则$\overrightarrow{AE}$•$\overrightarrow{OF}$等于( )