题目内容
x≥0，y≥0及x+y≤2所围成的平面区域的面积是 ．
考点：二元一次不等式（组）与平面区域
专题：不等式的解法及应用
分析：作出不等式组对应的平面区域，根据平面区域即可求出面积．
解答：
解：
作出不等式组对应的平面区域如图
则对应的平面区域为三角形OAB，（为正方形）．
其中A（2，0），B（0，2），
∴三角形OAB的面积为
×2×2=2，
故答案为：2．
作出不等式组对应的平面区域如图则对应的平面区域为三角形OAB，（为正方形）．
其中A（2，0），B（0，2），
∴三角形OAB的面积为
| 1 |
| 2 |
故答案为：2．
点评：本题主要考查二元一次不等式组表示平面区域，利用数形结合作出对应的图象是解决本题的关键．
练习册系列答案
相关题目
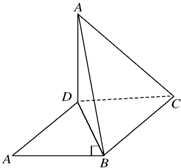如图，平行四边形ABCD中，AB⊥BD，沿BD将△ABD折起到A′BD，使面A′BD⊥面BCD，连接A′C，则在四面体A′BCD的四个面中，互相垂直的平面有（ ）①面ABD⊥面BCD；
②面A′CD⊥面ABD；
③面A′BC⊥面BCD；
④面ACD⊥面ABC．
| A、1个 | B、2个 | C、3个 | D、4个 |
函数f（x）=ax+
-a（a∈R，a≠0）在x=3处的切线方程与直线（2a-1）x-2y+3=0平行且f（3）=3，若方程f（x）=t（x2-2x+3）|x|有三个解，则实数t的取值范围为 ．
| b |
| x-1 |
设a、b∈z，且a≠0，则（a-b）a2＜0，且a＜b的（ ）条件．
| A、充分不必要 |
| B、必要而不充分 |
| C、充要 |
| D、既不充分也不必要 |
已知点D为等腰直角三角形ABC斜边AB的中点，则下列等式中不恒成立的是（ ）
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、(
|
设f（x）与g（x）是定义在同一区间[m，n]上的两个函数，若函数y=f（x）-g（x）在x∈[m，n]上有两个不同的零点，则称f（x）和g（x）在[m，n]上是“相关函数”，区间[m，n]是“相关区间”．若f（x）=-x2+tx-3与g（x）=2x+t在[2，4]上是“相关函数”，则实数t的取值范围是（ ）
A、（4+2
| ||||
B、{4+2
| ||||
C、（-∞，4-2
| ||||
D、（4+2
|
命题“若α=
，则tan α=1”的逆否命题是（ ）
| π |
| 4 |
A、若α≠
| ||
B、若α=
| ||
C、若tan α≠1，则α≠
| ||
D、若tan α≠1，则α=
|