题目内容
下列说法:
①“?x∈R”使“2x>3”的否定“?x∈R,使2x<3
②把函数y=sin2x图象上所有点向右平移
个单位得到y=sin(2x-
)的图象
③命题“函数f(x)在x=x0处有极值,则f′(x)=0”的否命题是真命题;
④f(x)是(-∞,0)∪(0,+∞)上的奇函数,x>0时的解析式是f(x)=2x,则x<0时的解析式为f(x)=-2-x
其中所有说法正确的是 .
①“?x∈R”使“2x>3”的否定“?x∈R,使2x<3
②把函数y=sin2x图象上所有点向右平移
| π |
| 3 |
| π |
| 3 |
③命题“函数f(x)在x=x0处有极值,则f′(x)=0”的否命题是真命题;
④f(x)是(-∞,0)∪(0,+∞)上的奇函数,x>0时的解析式是f(x)=2x,则x<0时的解析式为f(x)=-2-x
其中所有说法正确的是
考点:命题的真假判断与应用
专题:简易逻辑
分析:①利用命题的否定即可判断出;
②把函数y=sin2x图象上所有点向右平移
个单位得到y=sin(2(x-
))=sin(2x-
)的图象,即可判断出;
③举反例:函数f(x)=x3,虽然在x=0处没有极值,但是f′(0)=0,因此不正确;
④由于x>0时的解析式是f(x)=2x,则x<0时,-x>0,可得f(-x)=2-x,由于f(x)是(-∞,0)∪(0,+∞)上的奇函数,可得f(x)=-f(-x)即可得出.
②把函数y=sin2x图象上所有点向右平移
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
③举反例:函数f(x)=x3,虽然在x=0处没有极值,但是f′(0)=0,因此不正确;
④由于x>0时的解析式是f(x)=2x,则x<0时,-x>0,可得f(-x)=2-x,由于f(x)是(-∞,0)∪(0,+∞)上的奇函数,可得f(x)=-f(-x)即可得出.
解答:
解:①“?x∈R”使“2x>3”的否定“?x∈R,使2x≤3”,因此不正确;
②把函数y=sin2x图象上所有点向右平移
个单位得到y=sin(2(x-
))=sin(2x-
)的图象,因此不正确;
③命题“函数f(x)在x=x0处有极值,则f′(x)=0”的否命题是“函数f(x)在x=x0处没有极值,则f′(x)≠0”是真命题,例如函数f(x)=x3,虽然在x=0处没有极值,但是f′(0)=0,因此不正确;
④∵x>0时的解析式是f(x)=2x,则x<0时,-x>0,∴f(-x)=2-x,由于f(x)是(-∞,0)∪(0,+∞)上的奇函数,∴f(x)=-f(-x)=-2-x,因此正确.
其中所有说法正确的是 ④.
故答案为:④.
②把函数y=sin2x图象上所有点向右平移
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
③命题“函数f(x)在x=x0处有极值,则f′(x)=0”的否命题是“函数f(x)在x=x0处没有极值,则f′(x)≠0”是真命题,例如函数f(x)=x3,虽然在x=0处没有极值,但是f′(0)=0,因此不正确;
④∵x>0时的解析式是f(x)=2x,则x<0时,-x>0,∴f(-x)=2-x,由于f(x)是(-∞,0)∪(0,+∞)上的奇函数,∴f(x)=-f(-x)=-2-x,因此正确.
其中所有说法正确的是 ④.
故答案为:④.
点评:本题考查了简易逻辑的判定、三角函数的平移变换、函数取得极值的充要条件、函数的奇偶性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数与中位数分别是( ) 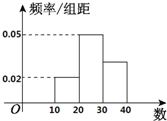

| A、25;25 |
| B、26;25 |
| C、26;26 |
| D、25;26 |