题目内容
已知点D为等腰直角三角形ABC斜边AB的中点，则下列等式中不恒成立的是（ ）
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、(
|
考点：平面向量数量积的运算
专题：平面向量及应用
分析：根据向量的数量积运算、平行四边形法则、投影的定义、射影定理、向量垂直与数量积的关系加以逐个判断即可
解答：
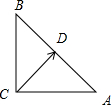解：A．由
=
（
+
）≠
+
，因此不恒成立．
B．由投影的定义和射影定理可得
•
=|
||
=|
|2，因此恒成立；
C．同B可知：正确；
D．由等腰直角三角形ABC，∴CB=CA，∴
•
，∴
2-
2=(
+
)•(
-
)=0，因此恒成立；
综上只有：A不正确．
故选：A．
解：A．由| CD |
| 1 |
| 2 |
| CA |
| CB |
| ||
|
|
|
B．由投影的定义和射影定理可得
| AC |
| AB |
| AD |
| AB| |
| AC |
C．同B可知：正确；
D．由等腰直角三角形ABC，∴CB=CA，∴
| CD |
| BA |
| CA |
| CB |
| CA |
| CB |
| CA |
| CB |
综上只有：A不正确．
故选：A．
点评：本题考查了向量的数量积运算、平行四边形法则、投影的定义、射影定理、向量垂直与数量积的关系，属于基础题．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
在△ABC中，AC=如图所示是一样本的频率分布直方图，则由图形中的数据，可以估计众数与中位数分别是（ ）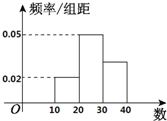 
| A、25；25 |
| B、26；25 |
| C、26；26 |
| D、25；26 |
动点P（x，0），定点A（0，2），B（4，1），则|PA|+|PB|的最小值为（ ）
A、
| ||
B、3
| ||
| C、4 | ||
| D、5 |