题目内容
设f(x)与g(x)是定义在同一区间[m,n]上的两个函数,若函数y=f(x)-g(x)在x∈[m,n]上有两个不同的零点,则称f(x)和g(x)在[m,n]上是“相关函数”,区间[m,n]是“相关区间”.若f(x)=-x2+tx-3与g(x)=2x+t在[2,4]上是“相关函数”,则实数t的取值范围是( )
A、(4+2
| ||||
B、{4+2
| ||||
C、(-∞,4-2
| ||||
D、(4+2
|
考点:函数零点的判定定理
专题:函数的性质及应用
分析:由题意可知,函数y=f(x)-g(x)在x∈[m,n]上有两个不同的零点,即方程f(x)-g(x)=0在[m,n]上有两个互异的实数根,依此即可将问题解决.
解答:
解:由已知得:若f(x)=-x2+tx-3与g(x)=2x+t在[2,4]上是“相关函数”.
即-x2+tx-3-2x-t=0在[2,4]上有两个互异实数根.
即x2+(2-t)x+t+3=0在[2,4]上有两个互异实数根.令f(x)=x2+(2-t)x+3+t.
则只需
,解得
,所以4+2
<t≤9即为所求.
故选B
即-x2+tx-3-2x-t=0在[2,4]上有两个互异实数根.
即x2+(2-t)x+t+3=0在[2,4]上有两个互异实数根.令f(x)=x2+(2-t)x+3+t.
则只需
|
|
| 6 |
故选B
点评:本题考查了利用函数的零点概念定义的新定义问题,通过对新定义的理解,最终将问题转化为方程的根的分布问题来解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数与中位数分别是( ) 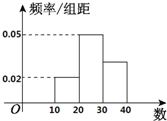

| A、25;25 |
| B、26;25 |
| C、26;26 |
| D、25;26 |