题目内容
设a、b∈z，且a≠0，则（a-b）a2＜0，且a＜b的（ ）条件．
| A、充分不必要 |
| B、必要而不充分 |
| C、充要 |
| D、既不充分也不必要 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据不等式的性质，结合充分条件和必要条件的定义即可得到结论．
解答：
解：∵a≠0，∴不等式（a-b）a2＜0，等价为a-b＜0，即a＜b，
则“（a-b）a2＜0”是“a＜b”的充分必要条件，
故选：C
则“（a-b）a2＜0”是“a＜b”的充分必要条件，
故选：C
点评：本题主要考查充分条件和必要条件的判断，根据不等式的关系是解决本题的关键．
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
已知抛物线x2=2py（p＞0）的焦点为F，A，B，C都是抛物线上的点，满足
+
+
=
，则kAB+kBC+kAC=（ ）
| FA |
| FB |
| FC |
| 0 |
| A、0 | ||
B、
| ||
| C、1 | ||
| D、不能确定 |
如图所示是一样本的频率分布直方图，则由图形中的数据，可以估计众数与中位数分别是（ ）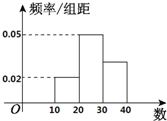 
| A、25；25 |
| B、26；25 |
| C、26；26 |
| D、25；26 |