题目内容
10.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,过点F2倾斜角为$\frac{π}{6}$的直线与双曲线的左支交于M点,且满足($\overrightarrow{{F}_{1}M}$+$\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{M{F}_{2}}$=0,则双曲线的离心率为( )| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $\sqrt{3}$+1 | D. | $\frac{\sqrt{3}+1}{2}$ |
分析 由题意可知($\overrightarrow{{F}_{1}M}$+$\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{M{F}_{2}}$=0,则△MF1F2为等腰三角形,则丨MF1丨=丨F1F2丨=2c,由直线的倾斜角的对顶角相等,则∠F1F2D=$\frac{π}{6}$,求得丨MF2丨,丨MF1丨,利用双曲线的定义,即可求得a和c的关系,求得双曲线的离心率.
解答 解:由题意可知:取MF2得中点D,连接MF1,
由$\overrightarrow{{F}_{1}M}$+$\overrightarrow{{F}_{1}{F}_{2}}$=2$\overrightarrow{{F}_{1}D}$,
则由2$\overrightarrow{{F}_{1}D}$•$\overrightarrow{M{F}_{2}}$=0,
则$\overrightarrow{{F}_{1}D}$⊥$\overrightarrow{M{F}_{2}}$,
∴△MF1F2为等腰三角形,则丨MF1丨=丨F1F2丨=2c,∠F1F2D=$\frac{π}{6}$,
则丨F2D丨=丨F1F2丨cos$\frac{π}{6}$=$\sqrt{3}$c,
丨MF2丨=2丨F2D丨=2$\sqrt{3}$c,
由双曲线的定义可知:丨MF2丨-丨MF1丨=2a,即a=($\sqrt{3}$-1)c,
双曲线的离心率e=$\frac{c}{a}$=$\frac{1}{\sqrt{3}-1}$=$\frac{\sqrt{3}+1}{2}$,
故选D.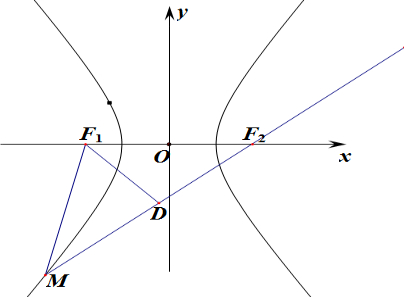
点评 本题考查双曲线的简单几何性质,考查向量的运算,考查数形结合思想,属于中档题.

练习册系列答案
相关题目
3.${(x-\frac{1}{x})^6}$的展开式中含x2的项的系数是( )
| A. | -20 | B. | 20 | C. | -15 | D. | 15 |