题目内容
5.过抛物线C:y2=4x焦点F的直线交抛物线C于A、B两点,|AB|=8,过线段AB的中点作y轴的垂线,垂足为P,则|$\overrightarrow{PA}$|2+|$\overrightarrow{PB}$|2=( )| A. | 36 | B. | 40 | C. | 50 | D. | 52 |
分析 由抛物线焦点弦公式可知丨CP丨=3,利用余弦定理,分别求得丨$\overrightarrow{PA}$丨2和丨$\overrightarrow{PB}$丨2,则丨$\overrightarrow{PA}$丨2+丨$\overrightarrow{PB}$丨2=32+2丨$\overrightarrow{PC}$丨2=50.
解答 解:抛物线C:y2=4x焦点(1,0),设AB的中点C,
由抛物线的焦点弦公式可知丨AB丨=2丨CP丨+2p,
则丨CP丨=3,
由余弦定理可知:丨$\overrightarrow{PA}$丨2=丨$\overrightarrow{AC}$丨2+丨$\overrightarrow{PC}$丨2-2丨$\overrightarrow{AC}$丨丨$\overrightarrow{PC}$丨cos∠ACP,
即丨$\overrightarrow{PA}$丨2=42+丨$\overrightarrow{PC}$丨2-2×4丨$\overrightarrow{PC}$丨cos∠ACP,
同理可得:丨$\overrightarrow{PB}$丨2=42+丨$\overrightarrow{PC}$丨2-2×4丨$\overrightarrow{PC}$丨cos∠BCP,
由∠ACP+∠BCP=π,则cos∠BCP=-cos∠ACP,
∴丨$\overrightarrow{PA}$丨2+丨$\overrightarrow{PB}$丨2=32+2丨$\overrightarrow{PC}$丨2=50,
∴丨$\overrightarrow{PA}$丨2+丨$\overrightarrow{PB}$丨2=50,
故选C.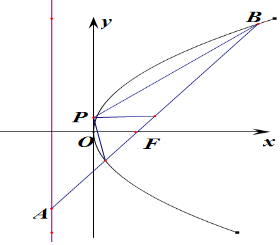
点评 本题考查抛物线的焦点弦公式,考查余弦定理的应用,考查计算能力,属于中档题.

| A. | 2α+β=$\frac{π}{2}$ | B. | 2α-β=$\frac{π}{2}$ | C. | α+2β=$\frac{π}{2}$ | D. | α-2β=$\frac{π}{2}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
 某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲,乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在(195,210]内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,如图是乙流水线样本的频率分布直方图.
某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲,乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在(195,210]内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,如图是乙流水线样本的频率分布直方图.甲流水线样本的频数分布表
| 质量指标值 | 频数 |
| (190,195] | 9 |
| (195,200] | 10 |
| (200,205] | 17 |
| (205,210] | 8 |
| (210,215] | 6 |
(Ⅱ)若将频率视为概率,某个月内甲,乙两条流水线均生产了5000件产品,则甲,乙两
条流水线分别生产出不合格品约多少件?
(Ⅲ)根据已知条件完成下面2×2列联表,并回答是否有85%的把握认为“该企业生产的这
种产品的质量指标值与甲,乙两条流水线的选择有关”?
| 甲生产线 | 乙生产线 | 合计 | |
| 合格品 | |||
| 不合格品 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $\sqrt{3}$+1 | D. | $\frac{\sqrt{3}+1}{2}$ |
 如图,一块长宽分别为30M、40M的矩形草地,其中间及四角是半径为10M的圆和扇形花圃,随意向草地浇水,则浇在花圃中的概率为( )
如图,一块长宽分别为30M、40M的矩形草地,其中间及四角是半径为10M的圆和扇形花圃,随意向草地浇水,则浇在花圃中的概率为( )| A. | $\frac{π}{12}$ | B. | $1-\frac{π}{6}$ | C. | $\frac{π}{6}$ | D. | $1-\frac{π}{12}$ |
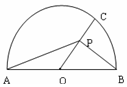 如图,半圆的直径AB=4,O为圆心,C为半圆上不同A,B的任意一点,若P为半径OC上的动点,则($\overrightarrow{PA}+\overline{PB}$)•$\overline{PC}$的最小值等于( )
如图,半圆的直径AB=4,O为圆心,C为半圆上不同A,B的任意一点,若P为半径OC上的动点,则($\overrightarrow{PA}+\overline{PB}$)•$\overline{PC}$的最小值等于( )